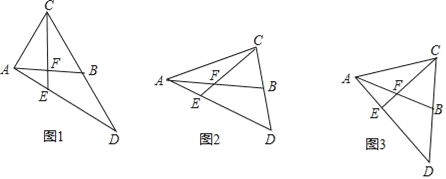
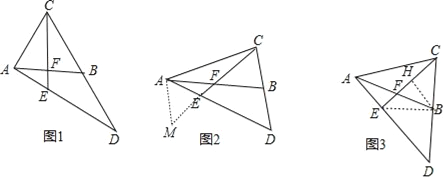
【题目】已知,在等腰△ABC中,AB=AC,F为AB边上的中点,延长CB至D,使得BD=BC,连接AD交CF的延长线于E.
(1)如图1,若∠BAC=60°,求证:△CED为等腰三角形
(2)如图2,若∠BAC≠60°,(1)中结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,当![]() = 是(直接填空),△CED为等腰直角三角形.
= 是(直接填空),△CED为等腰直角三角形.
参考答案:
【答案】(1)证明见解析;(2)成立.理由见解析;(3)![]() .
.
【解析】试题分析:(1)如图1,先证明△ABC为等边三角形得到∠ACB=∠ABC=60°,AB=BC,再证明∠D=∠DCE=30°,然后根据等腰三角形的判定定理得到△CED为等腰三角形;
(2)延长CF到M使FM=CF,连接AM,如图2,先证明△AMF≌△BCF得到AM=BC,∠M=∠BCF,再证明△AMC≌△BDA得到∠M=∠D,所以∠D=∠DCE,于是可判断△CED为等腰三角形;
(3)作BH⊥CE于H,连接BE,如图3,由(2)得△CED为等腰三角形,当∠BCE=45°时,△CED为等腰直角三角形,则EB⊥CD,设BH=x,则CH=EH=x,BC=![]() x,易证得△AEF≌△BHF,则EF=HF=
x,易证得△AEF≌△BHF,则EF=HF=![]() HE=
HE=![]() x,再利用勾股定理计算出BF=
x,再利用勾股定理计算出BF=![]() x,所以AB=2BF=
x,所以AB=2BF=![]() x,然后计算出
x,然后计算出![]() 的值.
的值.
试题解析:(1)如图1,
∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,AB=BC,
而BC=BD,∴AB=BD,∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,∴∠D=30°,
∵F点AB的中点,∴CF平分∠ACB,∴∠ACE=∠DCE=30°,∴∠D=∠DCE,
∴△CED为等腰三角形;
(2)成立.
延长CF到M使FM=CF,连接AM,如图2,
在△AMF和△BCF中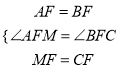 ,∴△AMF≌△BCF,∴AM=BC,∠M=∠BCF,
,∴△AMF≌△BCF,∴AM=BC,∠M=∠BCF,
∵BC=BD,∴AM=BD,
∵∠M=∠BCF,∴AM∥CD,∴∠MAC+∠ACB=180°,
而∠DBA+∠ABC=180°,∠ABC=∠ACB,∴∠MAC=∠DBA,
在△AMC和△BDA中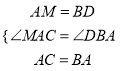 ,∴△AMC≌△BDA,∴∠M=∠D,∴∠D=∠DCE,
,∴△AMC≌△BDA,∴∠M=∠D,∴∠D=∠DCE,
∴△CED为等腰三角形;
(3)作BH⊥CE于H,连接BE,如图3,
由(2)得△CED为等腰三角形,当∠BCE=45°时,△CED为等腰直角三角形,
∴EB⊥CD,
设BH=x,则CH=EH=x,BC=![]() x,易证得△AEF≌△BHF,则EF=HF=
x,易证得△AEF≌△BHF,则EF=HF=![]() HE=
HE=![]() x,
x,
在△BFH中,BF=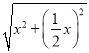 =
=![]() x,∴AB=2BF=
x,∴AB=2BF=![]() x,∴
x,∴![]() =
=![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.
求证:四边形AECF是平行四边形.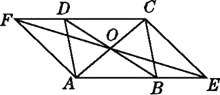
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列所给的四根已知长度的细木条中,能与长度为6cm,13cm的两根木条首尾相接钉成一个三角形木架的木条是( )
A. 6cm B. 7cm C. 13cm D. 20cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
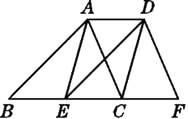
(1)求证:△ABC≌△DEF;
(2)试判断:四边形AECD的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.—2是4的一个平方根B.立方根等于它本身的数只有1和0
C.平方根等于它本身的数只有0D.平方等于它本身的数只有0和1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,直线l交CD边于点E,连接BE.
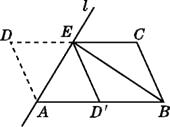
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④
 <a<
<a< ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
相关试题

