【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.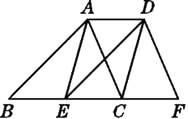
(1)求证:△ABC≌△DEF;
(2)试判断:四边形AECD的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,
∴BC=EF.
在△ABC和△DEF中,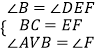
∴△ABC≌△DEF.
(2)解:四边形AECD是平行四边形.
理由:∵△ABC≌△DEF,∴AC=DF.
∵∠ACB=∠F,∴AC∥DF,
∴四边形ACFD是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,∴四边形AECD是平行四边形
【解析】(1)根据平行线的性质证出∠B=∠DEF.,再根据BE=EC=CF得出BC=EF,然后利用全等三角形的判定即可证得结论。
(2)根据全等三角形的性质得出AC=DF,再根据平行线的判定证明AC∥DF,可得到四边形ACFD是平行四边形,再根据平行四边形的性质得出AD∥CF,AD=CF,从而可证明AD=EC,然后再根据平行四边形的判定证得结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点(﹣1,﹣3)且与直线y=1﹣x平行的直线表达式是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.
求证:四边形AECF是平行四边形.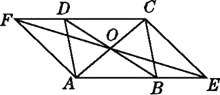
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列所给的四根已知长度的细木条中,能与长度为6cm,13cm的两根木条首尾相接钉成一个三角形木架的木条是( )
A. 6cm B. 7cm C. 13cm D. 20cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在等腰△ABC中,AB=AC,F为AB边上的中点,延长CB至D,使得BD=BC,连接AD交CF的延长线于E.
(1)如图1,若∠BAC=60°,求证:△CED为等腰三角形
(2)如图2,若∠BAC≠60°,(1)中结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,当
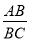 = 是(直接填空),△CED为等腰直角三角形.
= 是(直接填空),△CED为等腰直角三角形.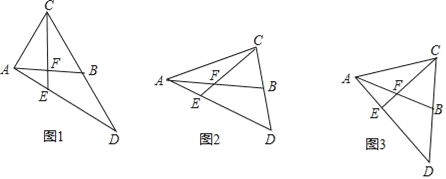
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.—2是4的一个平方根B.立方根等于它本身的数只有1和0
C.平方根等于它本身的数只有0D.平方等于它本身的数只有0和1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,直线l交CD边于点E,连接BE.
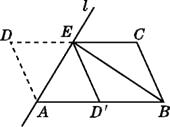
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
相关试题

