【题目】如图，在正方形网格上有一个△DEF ．
①作△DEF关于直线HG的轴对称图形；
②作△DEF的EF边上的高；
③若网格上的最小正方形边长为1，求△DEF的面积．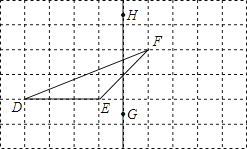

参考答案：

【答案】【解答】①如图所示，△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形；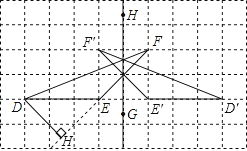

②如图所示，DH为EF边上的高线；
③△DEF的面积 ．
【解析】【分析①根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置，然后顺次连接即可；
②根据网格结构以及EF的位置，过点D作小正方形的对角线，与FE的延长线相交于H ， DH即为所求作的高线；
③DE为底边，点F到DE的距离为高，根据三角形的面积公式列式进行计算即可得解．
【考点精析】通过灵活运用轴对称图形，掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴即可以解答此题．

关闭