【题目】已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(﹣1,0). 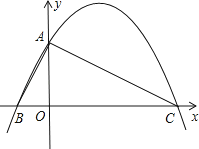
(1)求点C的坐标;
(2)求过A、B、C三点的抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标;
(4)在抛物线对称轴上,是否存在这样的点M,使得△MPC(P为上述(3)问中使S最大时的点)为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:在Rt△ABC中,AO⊥BC,OA=2,OB=1,
则:OC= ![]() =4,
=4,
∴C(4,0).
(2)
解:设抛物线的解析式:y=a(x+1)(x﹣4),代入点A的坐标,得:
a(0+1)(0﹣4)=2,a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+2,对称轴是:直线x=
x+2,对称轴是:直线x= ![]()
(3)
解:设直线AC的解析式为:y=kx+2,代入点C(4,0),得:
4k+2=0,k=﹣ ![]()
∴直线AC:y=﹣ ![]() x+2;
x+2;
过点P作PQ⊥x轴于H,交直线AC于Q,设P(m,﹣ ![]() m2+
m2+ ![]() m+2)、
m+2)、
∴S梯形AOHP= ![]() [2+(﹣
[2+(﹣ ![]() m2+
m2+ ![]() m+2)]m=﹣
m+2)]m=﹣ ![]() m3+
m3+ ![]() m2+2m,
m2+2m,
S△PHC= ![]() (4﹣m)(﹣
(4﹣m)(﹣ ![]() m2+
m2+ ![]() m+2)=
m+2)= ![]() m3﹣
m3﹣ ![]() m2+2m+4,
m2+2m+4,
S△AOC= ![]() ×4×2=4,
×4×2=4,
S=S梯形AOHP+S△PHC﹣S△AOC=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2,即 P(2,3)时,S的值最大
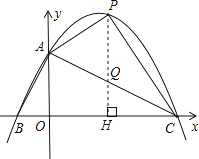
(4)
解:依题意,设M( ![]() ,b),已知P(2,3)、C(4,0),则有:
,b),已知P(2,3)、C(4,0),则有:
MP2=b2﹣6b+ ![]() 、MC2=b2+
、MC2=b2+ ![]() 、PC2=13;
、PC2=13;
当MP=MC时,b2﹣6b+ ![]() =b2+
=b2+ ![]() ,解得 b=
,解得 b= ![]() ;
;
当MP=PC时,b2﹣6b+ ![]() =13,解得 b=
=13,解得 b= ![]() ;
;
当MC=PC时,b2+ ![]() =13,解得 b=±
=13,解得 b=± ![]() ;
;
综上,存在符合条件的M点,且坐标为 ( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)Rt△ABC中,AO⊥BC,且知道了OA、OB的长,由射影定理能求出OC的长,也就得到了点C的坐标.(2)利用待定系数法即可确定抛物线的解析式,由x=﹣ ![]() 能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S=
能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S= ![]() ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.
ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家经销一种绿茶,用于装修门面已投资3000元,已知绿茶每千克成本50元,在第一个月的试销时间内发现,销量w(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如下表所示
销售单价x(元/kg)
…
70
75
80
85
90
…
销售量w(kg)
…
100
90
80
70
60
…
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量﹣成本﹣投资).
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围).并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700元,那么第二个月里应该确定销售单价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
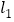 ∥
∥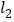 ,BE∥CF,BA⊥
,BE∥CF,BA⊥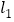 ,DC⊥
,DC⊥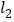 ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③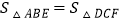 ;
;④四边形ABCD是矩形.其中说法正确的有( )
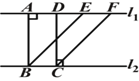
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…依此类推,则平行四边形AO4C5B的面积为( )

A.
 cm2 B.
cm2 B.  cm2 C.
cm2 C.  cm2 D.
cm2 D.  cm2
cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为( )

A.16
B.15
C.14
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-2)+(-3)+5
(2)
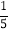 ×5÷
×5÷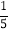 ×5
×5(3)12-7×(-4)+8÷(-2)
(4)-14+(2-5)2-2
(5)2÷(-2)+0÷7-(-8)×(-2)
(6)(-1)5×(-5)÷[(-3)2+2×(-5)].
相关试题

