【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )

A. 3 B. 6 C. 8 D. 9
参考答案:
【答案】D
【解析】
根据等边三角形,平行线的性质,和平行四边形的判定,并根据等腰梯形性质求解.
延长OD交AC于点G,
∵OE∥CG,OG∥CE,
∴四边形OGCE是平行四边形,有OE=CG,∠OGF=∠C=60°,
∵OF∥AB,
∴∠OFG=∠A=60°,
∴OF=OG,
∴△OGF是等边三角形,
∴OF=FG,
∵OD∥BC,
∴∠ADO=∠B=60°,
∴梯形OFAD是等腰梯形,有OD=AF,即OD+OE+OF=AF+FG+CG=AC=9.

故选:D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小方格都是边长为1的正方形
(1)求
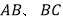 的长度.
的长度.(2)用勾股定理的知识证明:
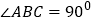 .
.
-
科目: 来源: 题型:
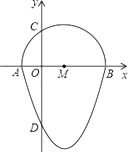
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其验证过程:
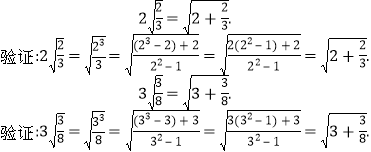
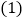 按照上述两个等式及其验证过程的基本思路,猜想
按照上述两个等式及其验证过程的基本思路,猜想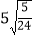 的变形结果并进行验证;
的变形结果并进行验证; 针对上述各式反应的规律,写出用
针对上述各式反应的规律,写出用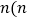 为任意自然数,且
为任意自然数,且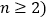 表示的等式,并说明它成立.
表示的等式,并说明它成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF其中正确的是( )
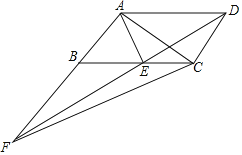
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
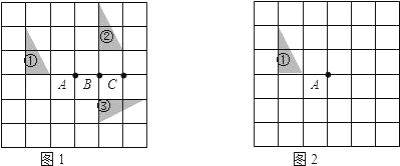
(1)在图1中,图①经过一次变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点(填“A”或 “B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.
相关试题

