【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
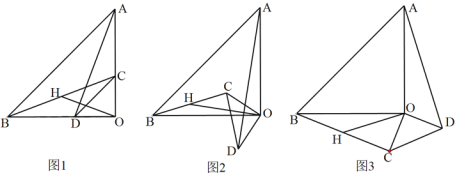
(1)如图1所示,求证:![]() 且
且![]()
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)首先证明△AOD≌△BOC(SAS),利用全等三角形的性质得到BC=AD,再利用直角三角形斜边中线的性质即可得到OH=![]() BC=
BC=![]() AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
(2)如图2中,延长OH到E,使得HE=OH,连接BE,通过证明△BEO≌△ODA,可得OH=![]() OE=
OE=![]() AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=
AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=![]() OE=
OE=![]() AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,

∴OC=OD,OA=OB,
在△AOD与△BOC中,
∵OA=OB,∠AOD=∠BOC,OD=OC,
∴△AOD≌△BOC(SAS),
∴BC=AD
∵H是BC中点,
∴OH=![]() BC=
BC=![]() AD.
AD.
∵△AOD≌△BOC
∴∠ADO=∠BCO,∠OAD=∠OBC,
∵点H为线段BC的中点,
∴∠OBH=∠HOB=∠OAD,
又∵∠OAD+∠ADO=90°,
∴∠ADO+∠BOH=90°,
∴OH⊥AD;
(2)解:结论:OH⊥AD,OH=![]() AD
AD

证明:如图2中,延长OH到E,使得HE=OH,连接BE,
易证△BEO≌△ODA,
∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOH=∠EOB+∠AOH=90°,
∴OH⊥AD.
如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA,

∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOG=∠EOB+∠AOG=90°,
∴∠AGO=90°,
∴OH⊥AD.
-
科目: 来源: 题型:
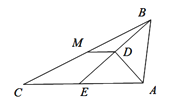
查看答案和解析>>【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=
 CE;
CE; (2)若AD=6,BD=8,DM=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别平分
分别平分 和
和 ,交
,交 于点
于点 ,线段
,线段 相交于点M.
相交于点M.(1)求证:
 ;
;(2)若
 ,则
,则 的值是__________.
的值是__________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】过□ABCD对角线交点O作直线m,分别交直线AB于点E,交直线CD于点F,若AB=4,AE=6,则DF的长是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线
 上一点
上一点 为端点作射线
为端点作射线 ,使
,使 ,将一个直角三角形的直角顶点放在点
,将一个直角三角形的直角顶点放在点 处(注:
处(注: )
) 如图①,若直角三角板
如图①,若直角三角板 的一边
的一边 放在射线
放在射线 上,则
上,则 .
.
 如图②,将直角三角板
如图②,将直角三角板 绕点
绕点 逆时针方向转动到某个位置,若
逆时针方向转动到某个位置,若 恰好平分
恰好平分 ,求
,求 的度数;
的度数;
 如图③,将直角三角板
如图③,将直角三角板 绕点
绕点 转动,如果
转动,如果 始终在
始终在 的内部,试猜想
的内部,试猜想 与
与 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;②图中有2对互补的角;③若∠BAE=100°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和的最大值为15,最小值为11.其中说法正确的个数有( )
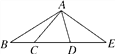
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

