【题目】如图，在Rt△ACB中，∠A=30°，过点B、C的⊙O交AB于D，交AC于E，点F在AE上，连接DE、DC、BE和DF，已知BC=EC，AD=AF．

（1）求证：DF是⊙O的切线；

（2）当BC=4时，求弦CD的长．

参考答案：

【答案】（1）证明见解析；（2）CD=2 ．

【解析】试题分析：（1）连接半径OD，可求得∠ODB=15°，∠ADF=75°，进一步可求得∠ODF=90°，可证得结论；（2）先求出BE，证明△ADC∽△AEB，有，可求出CD的长．

试题解析：（1）如图，连接半径OD，

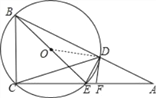
∵∠A=30°，AF=AD，

∴∠ADF=75°，

∵BE为直径，BC=EC，

∴∠CBE=45°，且∠ABC=60°，

∴∠OBD=∠ODB=15°，

∴∠ODF=180°﹣（∠ODB+∠ADF）=90°，

∴DF是⊙O的切线；

（2）在Rt△BCE中，BC=CE=4，

∴BE=，

∵∠A=30°，

∴AB=2BC=8，AC=，

又∠ABE=∠DCA，∠A=∠A，

∴△ADC∽△AEB，

∴，即，

解得CD=．

关闭