【题目】(2016广东省梅州市第20题)
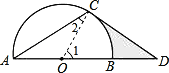
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

参考答案:
【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、连接OC,根据等腰三角形的性质得出∠CAD=∠D=30°,根据OA=OC得出∠2=∠CAD =30°,从而得出∠OCD=∠ACD —∠ACO=90°;(2)、首先求出扇形BOC的面积,根据Rt△OCD的三角函数得出CD的长度,从而求出Rt△OCD的面积,然后求出阴影部分的面积.
试题解析:(1)、连接OC. ∵AC=CD,∠ACD=120°, ∴∠CAD=∠D=30°.
∵OA=OC, ∴∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° )
∴∠OCD=∠ACD —∠ACO=90°,即OC⊥CD. ∴CD是⊙O的切线.
(2)、由(1)知∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° ), ∴∠1=60°.(或∠COD =60°)
∴![]() . 在Rt△OCD中,∵
. 在Rt△OCD中,∵![]() ,
,![]() ∴
∴![]() .
.
∴![]() ∴图中阴影部分的面积为
∴图中阴影部分的面积为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD,仅从下列条件中任取两个加以组合,使得ABCD是平行四边形,一共有多少种不同的组合? AB∥CD BC∥AD AB=CD BC=AD( )
A.2组
B.3组
C.4组
D.6组 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6与x轴y轴分别交于点E,F.点E的坐标为(-8,0),点A的坐标为(-6,0).
(1)求K的值;
(2)若点P(x,y)是第二象限内该直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,△OPA的面积为
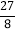 ,并说明理由.
,并说明理由.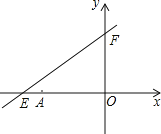
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条河的水流速度1.5km/h,某船在静水中的速度是vkm/h,则该船在这条河中逆流行驶的速度是( )
A. (v+1.5)km/h B. (v-1.5)km/h C. (v+3)km/h D. (v-3)km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,且相似比为2∶3,则△ABC与△DEF的对应高之比为( )
A. 2∶3 B. 3∶2 C. 4∶9 D. 9∶4
-
科目: 来源: 题型:
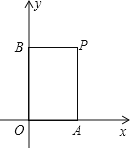
查看答案和解析>>【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点。例如,图中过点p分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点p是和谐点。
判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
若和谐点P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣x﹣2=0的解是( )
A.x1=﹣1,x2=﹣2
B.x1=1,x2=﹣2
C.x1=1,x2=2
D.x1=﹣1,x2=2
相关试题

