搜索
【题目】观察下面三行数
表示出每行数的第
个数，并计算这三个数的和；
表示出每行数的第
个数.
参考答案：
【答案】（1）4098；（2）
；
；
.
【解析】
（1）观察第一行数得到后面一个数是前一个数的-2倍，由此得出第一行的第n个数；观察发现同位置的第二行数比第一行数大1，同位置的第三行数是第一行数的2倍大1.；根据各行的表达式求出第10个数，然后相加即可得解．
（2）根据（1）中发现的规律，即可解答．
解：（1）每行数的第
个数分别为
；
；
，
三个数和=
答：三个数的和等于4098.
观察第一行数得到后面一个数是前一个数的-2倍，由此得出第一行的第n个数为；观察发现同位置的第二行数比第一行数大1，第二行的第n个数为，同位置的第三行数是第一行数的2倍大1.；第三行的第n个数为.
∴每行数的第
个数分别为；；.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝
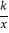(k≠0)的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH＝3，tan∠AOH＝
，点B的坐标为(m，－2)．(1)求△AHO的周长；
(2)求该反比例函数和一次函数的解析式．
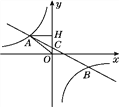
【答案】(1)△AHO的周长为12；(2) 反比例函数的解析式为y＝
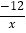，一次函数的解析式为y＝－
x＋1.【解析】试题分析: （1）根据正切函数，可得AH的长，根据勾股定理，可得AO的长，根据三角形的周长，可得答案；
（2）根据待定系数法，可得函数解析式．
试题解析：（1）由OH=3，tan∠AOH=
，得AH=4．即A（-4，3）．
由勾股定理，得
AO=
=5，△AHO的周长=AO+AH+OH=3+4+5=12；
（2）将A点坐标代入y=
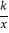（k≠0），得k=-4×3=-12，
反比例函数的解析式为y=
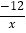；当y=-2时，-2=
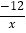，解得x=6，即B（6，-2）．将A、B点坐标代入y=ax+b，得
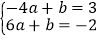，解得
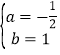，一次函数的解析式为y=-
x+1．考点：反比例函数与一次函数的交点问题．
【题型】解答题
【结束】
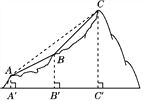
23【题目】如图，点A，B，C表示某旅游景区三个缆车站的位置，线段AB，BC表示连接缆车站的钢缆，已知A，B，C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米，310米，710米，钢缆AB的坡度i1＝1∶2，钢缆BC的坡度i2＝1∶1，景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？(注：坡度i是指坡面的铅直高度与水平宽度的比)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（ ）
A. 2 B.
C. 
D. 2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E是对角线BD上一点，且满足BE=BC．连接CE并延长交AD于点F，连接AE，过B点作BG⊥AE于点G，延长BG交AD于点H．在下列结论中：
①AH=DF； ②∠AEF=45°； ③S四边形EFHG=S△DEF+S△AGH，
其中正确的结论有_____________________．(填正确的序号)
-
科目： 来源： 题型：
查看答案和解析>>【题目】
观察下图并填表（单位
）
梯形个数
n
图形周长
······
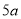
请通过计算说明第
个图形的周长比第
个图形的周长多多少
？
类比推理，直角三角形的三边长分别是
，请直接写出增加到第个直角三角形时，所得图形的周长为 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A，B，C表示某旅游景区三个缆车站的位置，线段AB，BC表示连接缆车站的钢缆，已知A，B，C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米，310米，710米，钢缆AB的坡度i1＝1∶2，钢缆BC的坡度i2＝1∶1，景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？(注：坡度i是指坡面的铅直高度与水平宽度的比)
【答案】钢缆AC的长度为1 000米．
【解析】试题分析：过点A作AE⊥CC′于点E，交BB′于点F，过点B作BD⊥CC′于点D，分别求出AE、CE，利用勾股定理求解AC即可．
试题解析：过点A作AE⊥CC′于点E，交BB′于点F，过点B作BD⊥CC′于点D，
则△AFB、△BDC、△AEC都是直角三角形，四边形AA′B′F，BB′C′D和BFED都是矩形，
∴BF=BB′-B′F=BB′-AA′=310-110=200，
CD=CC′-C′D=CC′-BB′=710-310=400，
∵i1=1：2，i2=1：1，
∴AF=2BF=400，BD=CD=400，
又∵EF=BD=400，DE=BF=200，
∴AE=AF+EF=800，CE=CD+DE=600，
∴在Rt△AEC中，AC=
（米）．答：钢缆AC的长度是1000米．
考点：解直角三角形的应用-坡度坡角问题．
【题型】解答题
【结束】
24【题目】如图①，AB为半圆的直径，O为圆心，C为圆弧上一点，AD垂直于过C点的切线，垂足为D，AB的延长线交直线CD于点E.
(1)求证：AC平分∠DAB；
(2)若AB＝4，B为OE的中点，CF⊥AB，垂足为点F，求CF的长；
(3)如图②，连接OD交AC于点G，若
，求sinE的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话。
⑴现有1，2，3，4，5，6，7，8，9共九个数字，请将它们分别填入图1的九个方格中，使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15．
⑵通过研究问题⑴，利用你发现的规律，将3，5，－7，1，7，－3，9，－5，－1
这九个数字分别填入图2的九个方格中，使得横、竖、斜对角的所有三个数的和都相等．
相关试题
