搜索
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：
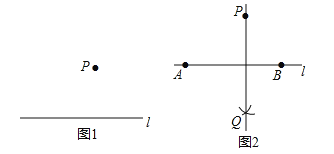
已知：直线l和l外一点P．（如图1）
求作：直线l的垂线，使它经过点P．
作法：如图2
（1）在直线l上任取两点A，B；
（2）分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；
（3）作直线PQ．
所以直线PQ就是所求的垂线．
请回答：该作图的依据是 ．
参考答案：
【答案】到线段两个端点的距离相等的点在线段的垂直平分线上（A、B都在线段PQ的垂直平分线上）．
【解析】
试题分析：到线段两个端点的距离相等的点在线段的垂直平分线上（A、B都在线段PQ的垂直平分线上），理由：如图，∵PA=PQ，PB=PB，∴点A、点B在线段PQ的垂直平分线上，∴直线AB垂直平分线段PQ，∴PQ⊥AB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学问题：计算
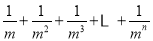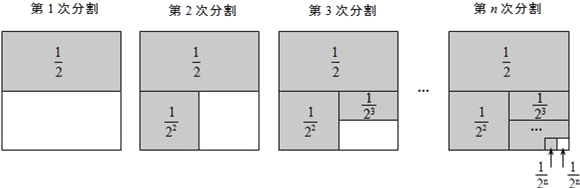
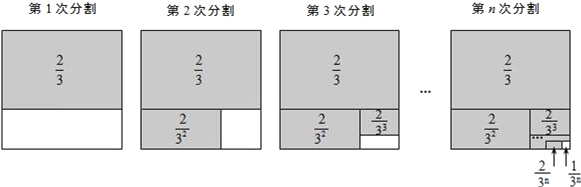
（其中m，n都是正整数，且m≥2，n≥1）．探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
．第1次分割，把正方形的面积二等分，其中阴影部分的面积为
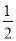；第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
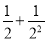；第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
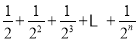，最后空白部分的面积是
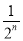．根据第n次分割图可得等式：
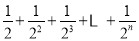=1﹣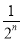
．
探究二：计算
．第1次分割，把正方形的面积三等分，其中阴影部分的面积为
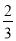；第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
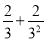；第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
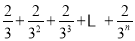，最后空白部分的面积是
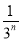．根据第n次分割图可得等式：
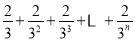=1﹣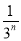
，两边同除以2，得
=
.
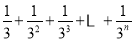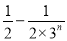探究三：计算
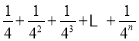．（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
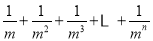．（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以，
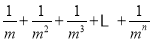= ．拓广应用：计算
． -
科目： 来源： 题型：
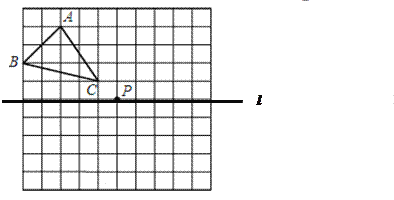
查看答案和解析>>【题目】如图，一个10×10网格，每个小正方形的边长均为1，每个小正方形的顶点叫格点，△ABC的顶点均在格点上．
（1）画出△ABC关于直线l的对称的△A1B1C1．
（2）画出△ABC关于点P的中心对称图形△A2B2C2．
（3）△A1B1C1与△A2B2C2组成的图形_______________（是或否）轴对称图形，如果是轴对称图形，请画出对称轴．
-
科目： 来源： 题型：
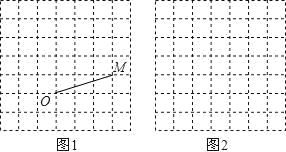
查看答案和解析>>【题目】图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．
（1）在图1中画出等腰直角三角形MON，使点N在格点上，且∠MON=90°；
（2）在图2中以格点为顶点画一个正方形ABCD，使正方形ABCD面积等于（1）中等腰直角三角形MON面积的4倍，并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形，且正方形ABCD面积没有剩余（画出一种即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.a2+a3=a5
B.a2a3=a6
C.a3+a2=a
D.（a2）3=a6 -
科目： 来源： 题型：
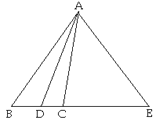
查看答案和解析>>【题目】如图，AD平分∠BAC，∠EAD＝∠EDA.
（1）∠EAC与∠B相等吗？为什么？
（2）若∠B＝50°,∠CAD︰∠E＝1︰3，求∠E的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列说法：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②三角形的三边a、b、c满足
+
=
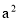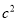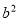,则
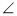C=90
；③△ABC中，若
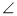A： 
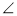B：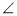 
C=1：5：6，则△ABC是直角三角形；④△ABC中，若a：b：c=1：2：
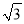，则这个三角形是直角三角形。其中，错误的说法的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
相关试题
