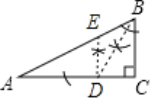
【题目】如图,Rt△ABC中,∠C=90°.

(1)在斜边AB上确定一点E,使点E到点B距离和点E到AC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BC=6,AC=8,点E到AC的距离为ED,求BD的长.
参考答案:
【答案】(1)如图,点E为所作;见解析;(2)BD=3![]() .
.
【解析】
(1)作出∠ABC的平分线BD交CD于点D,再过点D作AC的垂线交AB于点E即可;
(2)设DE的长为x,然后用x表示出BE、AE,由作图可知DE∥BC,则有△ADE∽△ACB,利用相似三角形的性质求出x,再根据勾股定理得到BDA.
(1)如图,点E为所作;
(2)设DE=BE=x,
在Rt△ABC中,AB=![]() =10,
=10,
∴AE=10﹣x,
∵DE∥BC,
∴△ADE∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=![]() ,
,
∴DE=![]() ,AE=
,AE=![]() ,
,
∴AD=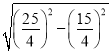 =5,
=5,
∴CD=3,
∴BD=![]() =3
=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一个四边形的草坪,AB与AD垂直,通过测量,获得如下数据:AB=12m,BC=14m,AD=5m,CD=3
 m,请你测算这块草坪的面积.(结果保留准确值)
m,请你测算这块草坪的面积.(结果保留准确值)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(用阴影表示).

(1)在图(a)中,画一个不含直角的三角形,使它的三边长都是有理数;
(2)在图(b)中,画一个直角三角形,使它的斜边长为
 ;
;(3)在图(c)中,画一个直角三角形,使它的斜边长为5,直角边长都是无理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在反比例函数y=
 (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD、ED⊥BD,连结AC、EC.已知AB=6,DE=2,BD=15,设CD=x.

(1)用含x的代数式表示AC+CE的值;(写出过程)
(2)请问点C满足条件 时,AC+CE的值最小;
(3)根据(2)中的结论,画图并标上数据,求代数式
 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,在△ABC外侧作∠ACM,使得∠ACM=
 ∠ABC,点D是射线CB上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是射线CB上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
(1)当点D与点B重合时,如图1所示,线段DF与EC的数量关系是 ;
(2)当点D运动到CB延长线上某一点时,线段DF和EC是否保持上述数量关系?请在图2中画出图形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠C是最小的一个内角,过顶点B的一条直线交AC于点D,直线BD将原三角形分割成两个等腰三角形△ABD和△BCD,△ABD中BD=AD,请探究∠A与∠C的数量关系,并说明理由.
相关试题

