【题目】如图,将边长为![]() 的正三角形纸片
的正三角形纸片![]() 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕![]() (如图①),点
(如图①),点![]() 为其交点.
为其交点.
(1)探求![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)如图②,若![]() 分别为
分别为![]() 上的动点.
上的动点.
①当![]() 的长度取得最小值时,求
的长度取得最小值时,求![]() 的长度;
的长度;
②如图③,若点![]() 在线段
在线段![]() 上,
上,![]() ,则
,则![]() 的最小值= .
的最小值= .

参考答案:
【答案】(1)AO=2OD,理由见解析;(2)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°,得到AO=OB,根据直角三角形的性质即可得到结论;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值,根据线段垂直平分线的想知道的BD=BD′,推出△BDD′是等边三角形,得到BN=![]() BD=
BD=![]() ,于是得到结论;
,于是得到结论;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′,即为QN+NP+PD的最小值.根据轴对称的定义得到∠Q′BN=∠QBN=30°,∠QBQ′=60°,得到△BQQ′为等边三角形,△BDD′为等边三角形,解直角三角形即可得到结论.
试题解析:(1)AO=2OD,
理由:∵△ABC是等边三角形,
∴∠BAO=∠ABO=∠OBD=30°,
∴AO=OB,
∵BD=CD,
∴AD⊥BC,
∴∠BDO=90°,
∴OB=2OD,
∴OA=2OD;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,

则此时PN+PD的长度取得最小值,
∵BE垂直平分DD′,
∴BD=BD′,
∵∠ABC=60°,
∴△BDD′是等边三角形,
∴BN=![]() BD=
BD=![]() ,
,
∵∠PBN=30°,
∴![]() ,
,
∴PB=![]() ;
;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,
连接Q′D′,即为QN+NP+PD的最小值.

根据轴对称的定义可知:∠Q′BN=∠QBN=30°,∠QBQ′=60°,
∴△BQQ′为等边三角形,△BDD′为等边三角形,
∴∠D′BQ′=90°,
∴在Rt△D′BQ′中,
D′Q′=![]() .
.
∴QN+NP+PD的最小值=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】要判断小强同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( )
A.方差
B.众数
C.平均数
D.中位数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点
 处测得正前方小岛
处测得正前方小岛 的俯角为
的俯角为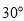 ,面向小岛方向继续飞行
,面向小岛方向继续飞行
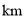 到达
到达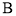 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为 .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
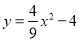 的图象与
的图象与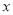 轴交于
轴交于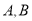 两点与
两点与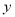 轴交于点
轴交于点 ,⊙
,⊙ 的半径为
的半径为 为⊙
为⊙ 上一动点.
上一动点.(1)点
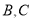 的坐标分别为
的坐标分别为 ( ),
( ), ( );
( );(2)是否存在点
 ,使得
,使得 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)连接
 ,若
,若 为
为 的中点,连接
的中点,连接 ,则
,则 的最大值= .
的最大值= .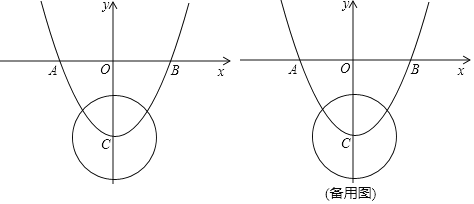
-
科目: 来源: 题型:
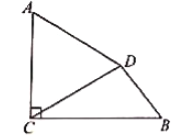
查看答案和解析>>【题目】如图,已知
 ,垂足为
,垂足为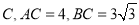 ,将线段
,将线段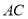 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 ,得到线段
,得到线段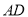 ,连接
,连接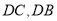 .
.
(1)线段
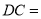 ;
;(2)求线段
 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】七边形的内角和是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
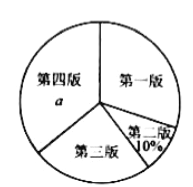

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,

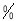 ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为  ;
; (2)请你补全条形统计图;
(3)若该校有
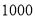 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
相关试题

