【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点与
两点与![]() 轴交于点
轴交于点![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 为⊙
为⊙![]() 上一动点.
上一动点.
(1)点![]() 的坐标分别为
的坐标分别为![]() ( ),
( ),![]() ( );
( );
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,若
,若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的最大值= .
的最大值= .
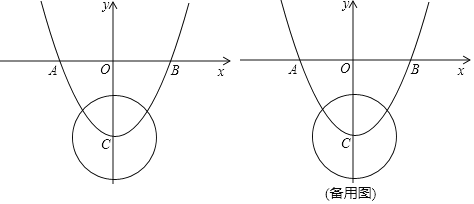
参考答案:
【答案】(1)3,0;0,-4;(2)(-1,-2)或((![]() ,
,![]() ),或(
),或(![]() ,-
,-![]() -4)或(--
-4)或(--![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)在抛物线解析式中令y=0可求得B点坐标,令x=0可求得C点坐标;
(2)①当PB与⊙相切时,△PBC为直角三角形,如图1,连接BC,根据勾股定理得到BC=5,BP2=2![]() ,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到
,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到![]() ,设OC=P2E=2x,CP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=
,设OC=P2E=2x,CP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=![]() ,EP2=
,EP2=![]() ,求得P2(
,求得P2(![]() ,-
,-![]() ),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
(3)如图2,当PB与⊙C相切时,OE的值最大,过E作EM⊥y轴于M,过P作PF⊥y轴于F,根据平行线等分线段定理得到ME=![]() (OB+PF)=
(OB+PF)=![]() ,OM=MF=
,OM=MF=![]() OF=
OF=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)在y=![]() x2-4中,令y=0,则x=±3,令x=0,则y=-4,
x2-4中,令y=0,则x=±3,令x=0,则y=-4,
∴B(3,0),C(0,-4);
(2)存在点P,使得△PBC为直角三角形,
①当PB与⊙相切时,△PBC为直角三角形,如图(2)a,连接BC,
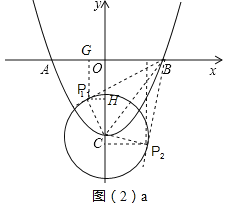
∵OB=3.OC=4,
∴BC=5,
∵CP2⊥BP2,CP2=![]() ,
,
∴BP2=2![]() ,
,
过P2作P2E⊥x轴于E,P2F⊥y轴于F,则△CP2F∽△BP2E,四边形OCP2B是矩形,
∴![]() ,
,
设OC=P2E=2x,CP2=OE=x,
∴BE=3-x,CF=2x-4,
∴![]() ,
,
∴x=![]() ,2x=
,2x=![]() ,
,
∴FP2=![]() ,EP2=
,EP2=![]() ,
,
∴P2(![]() ,
,![]() ),
),
过P1作P1G⊥x轴于G,P1H⊥y轴于H,
同理求得P1(-1,-2),
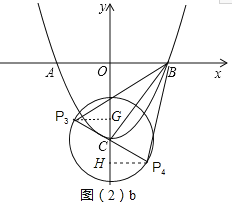
②当BC⊥PC时,△PBC为直角三角形,过P4作P4H⊥y轴于H,则△BOC∽△CHP4,
∴![]() ,
,
∴CH=![]() ,P4H=
,P4H=![]() ,
,
∴P4(![]() ,-
,-![]() -4);
-4);
同理P3(-![]() ,
,![]() );
);
综上所述:点P的坐标为:(-1,-2)或((![]() ,
,![]() ),或(
),或(![]() ,-
,-![]() -4)或(--
-4)或(--![]() ,
,![]() );
);
(3)如图(3),当PB与⊙C相切时,PB与y 轴的距离最大,OE的值最大,
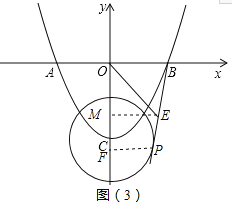
∵过E作EM⊥y轴于M,过P作PF⊥y轴于F,
∴OB∥EM∥PF,
∵E为PB的中点,
∴ME=![]() (OB+PF)=
(OB+PF)=![]() ,OM=MF=
,OM=MF=![]() OF=
OF=![]() ,
,
∴OE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
A.3.9753×109
B.0.39753×1010
C.39.753×1011
D.3.9753×1012 -
科目: 来源: 题型:
查看答案和解析>>【题目】要判断小强同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( )
A.方差
B.众数
C.平均数
D.中位数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点
 处测得正前方小岛
处测得正前方小岛 的俯角为
的俯角为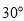 ,面向小岛方向继续飞行
,面向小岛方向继续飞行
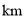 到达
到达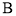 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为 .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
 的正三角形纸片
的正三角形纸片 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕 (如图①),点
(如图①),点 为其交点.
为其交点.(1)探求
 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;(2)如图②,若
 分别为
分别为 上的动点.
上的动点.①当
 的长度取得最小值时,求
的长度取得最小值时,求 的长度;
的长度;②如图③,若点
 在线段
在线段 上,
上, ,则
,则 的最小值= .
的最小值= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,垂足为
,垂足为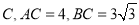 ,将线段
,将线段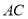 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 ,得到线段
,得到线段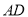 ,连接
,连接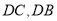 .
.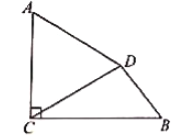
(1)线段
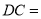 ;
;(2)求线段
 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】七边形的内角和是 .
相关试题

