【题目】如图,在平行四边形ABCD中,E,F,G,H分别是边AB,DC,BC,AD上的点,且AE=CF,BG=DH.求证:EF与GH互相平分.

参考答案:
【答案】见解析
【解析】
首先连接EH,FG,FH,GE,由在平行四边形ABCD中,E,F,G,H分别是边AB,DC,BC,AD上的点,且AE=CF,BG=DH,易证得△AEH≌△CFG,即可得FG=EH,继而可得HF=EG,即可证得四边形EGFH为平行四边形,继而证得EF与GH互相平分。
证明:连接EH,FG,FH,GE,

∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AB=CD,AD=BC,
∵AE=CF,BG=DH,
∴AH=CG,BE=DF,
在△AEH和△CFG中,
AE=CF
∠A=∠C
AH=CG
∴△AEH≌△CGF(SAS),
∴EH=GF,
同理:EG=HF,
∴四边形EGFH为平行四边形,
∴EF与GH互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A2019表示的数,是______.
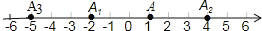
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,AD=9 cm.点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,当点P,Q运动_______s时,直线QP将四边形截出一个平行四边形.
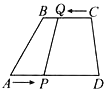
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
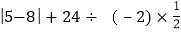 (2)(
(2)(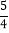 -
- )×(-
)×(- )
) (3)
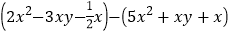 (4)(-2a2)3+ a8÷a2 +3a·a5
(4)(-2a2)3+ a8÷a2 +3a·a5(5)(2x-5)(2x+5)-2x(2x-3) (6)(3x+y)2-(3x-y)2
-
科目: 来源: 题型:
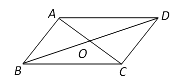
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC与BD相交于O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构成命题。
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G.
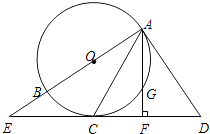
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
相关试题

