【题目】已知:如图,△ABC是边长为4cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
(1)求![]() 的面积;
的面积;
(2)当t为何值是,△PBQ是直角三角形?
(3)探究:是否存在某一时刻t,使四边形APQC的面积是![]() 面积的八分之五?如果存在,求出t的值;不存在请说明理由.
面积的八分之五?如果存在,求出t的值;不存在请说明理由.

参考答案:
【答案】(1)![]() ;(2)t=2或t=1;(3)不存在
;(2)t=2或t=1;(3)不存在
【解析】试题分析:(1)根据等边三角形的性质及三角形的面积公式求解即可;
(2)由题意此时P点和Q点移动距离为tcm,所以AP=BQ=tcm,BP=AB-AP=3-tcm,则在△PBQ中,∠B=60°,BP=3-t,BQ=t,分①当PQ⊥BC时,则∠BPQ=30°,②当PQ⊥BA时,则∠BQP=30°,两种情况,结合含30°角的直角三角形的性质求解即可;
(3)作QD⊥AB于D,则![]() ,根据
,根据![]() 的面积可表示出△BQD的面积,从而可得y与t的函数关系式,即可得到关于t的方程,由方程的根的判别式△
的面积可表示出△BQD的面积,从而可得y与t的函数关系式,即可得到关于t的方程,由方程的根的判别式△![]() 即可作出判断.
即可作出判断.
(1)![]() ;
;
(2)此时P点和Q点移动距离为tcm,所以AP=BQ=tcm,BP="AB-AP=3-tcm"
在△PBQ中,∠B=60°,BP=3-t,BQ=t
①当PQ⊥BC时,则∠BPQ=30°
∴BP=2BQ,即3-t=2t
∴t=1;
②当PQ⊥BA时,则∠BQP=30°
∴BQ=2BP,即2(3-t)=t
∴t=2
综上所述,t=2或t=1;
(3)作QD⊥AB于D,则![]()

∵![]()
![]()
∴![]()
当![]()
∴![]()
化简得:![]()
![]()
![]()
∴不存在这样的t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年某市将有5万名学生参加中考,为了解这些考生的数学成绩,中考后将从中抽取2000名考生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
A. 2000名考生是总体的一个样本
B. 每个考生是个体
C. 这5万名考生的数学中考成绩的全体是总体
D. 统计中采用的调查方式是普查
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个棱柱共有 15 条棱,那么它是__________棱柱,有___________个面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a2+3a3=5a5 B. a6÷a3=a2 C. (﹣a3)2=a6 D. (x+y)2=x2+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图.
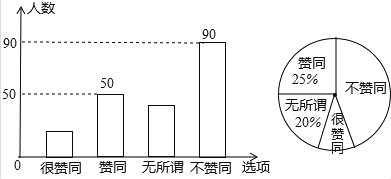
依据图中信息,得出下列结论:
(1)接受这次调查的家长人数为200人
(2)在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为162°
(3)表示“无所谓”的家长人数为40人
(4)随机抽查一名接受调查的家长,恰好抽到“很赞同”的家长的概率是
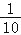 .
.其中正确的结论个数为( )
A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a4+a4=a 8B. (a3)4=a7
C. 12a6b4÷3a2b-2=4a4b2D. (-a3b)2=a6b2
-
科目: 来源: 题型:
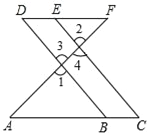
查看答案和解析>>【题目】根据题意结合图形填空:如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2(已知)
且∠1=∠3
∴∠2=∠3(等量代换)
∴ ∥
∴∠C=∠ABD
又∵∠C=∠D(已知)
∴ = (等量代换 )
∴AC∥DF .
相关试题

