【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B,分别向上平移2个单位,再向右平移1个单位,分别得到点A、B的对应点C、D,连接AC,BD,CD,得平行四边形ABDC.
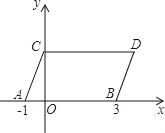
(1)直接写出点C,D的坐标;
(2)若在直线CD上存在点M,连接MA,MB,使S△MAB=2S△MBD,求出点M的坐标;
(3)若点P在直线BD上运动,连接PC,PO,请画出图形,写出∠CPO,∠DCP,∠BOP的数量关系,并说明理由.
参考答案:
【答案】(1)C(0,2),D(4,2);(2)M(2,2)或(6,2);(3)①当点P在BD上,∠CPO=∠DCP+∠BOP,见解析;②当点P在线段BD的延长线上时,∠CPO=∠BOP﹣∠DCP,见解析;③当点P在线段DB的延长线上时,∠CPO=∠DCP﹣∠BOP,见解析.
【解析】
(1)根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,
(2)先求出S△MAB=4,进而判断出SABCD=2S△MAB=2S△BCD,进而判断出S△MBD=2,再分两种情况即可得出结论;
(3)分三种情况,根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出结论.
解:(1)∵将A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S△MAB=![]() AB×OC=4,
AB×OC=4,
∵SABCD=AB×OC=8=2S△MAB=2S△BCD,
∵S△MAB=2S△MBD,
∴S△MBD=2,
当点M在边CD上时,
∴点M是CD的中点,
∴M(2,2),
当点M在CD的延长线上时,
利用对称性得,M'(6,2),
∴M(2,2)或(6,2);
(3)①当点P在BD上,如图1,
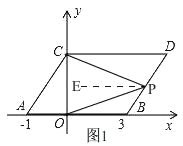
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
②当点P在线段BD的延长线上时,如图2,
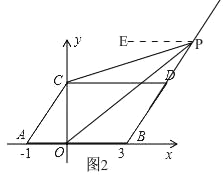
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE﹣∠CPE=∠BOP﹣∠DCP,
③当点P在线段DB的延长线上时,如图3,
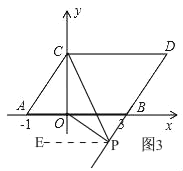
同(2)的方法得出∠CPO=∠DCP﹣∠BOP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.
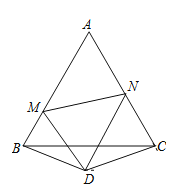
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
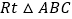 中,
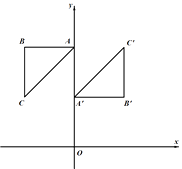
中,  ,AB=BC,A,B的坐标分别为
,AB=BC,A,B的坐标分别为  ,将
,将  绕点P旋转
绕点P旋转  后得到
后得到  ,其中点B的对应点
,其中点B的对应点  的坐标为
的坐标为  .
.
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
相关试题

