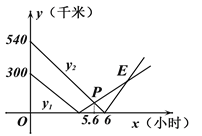
【题目】高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲乙两车离B的距离![]() 、
、![]() (千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
(千米)与行驶时间x(小时)之间的函数关系图象如图所示,交点P的横坐标为5.6,观察图象,给出下列结论:
①A、C之间的路程为840千米;②乙车比甲车每小时快30千米;③当乙车到A点时,甲车距离B点250千米;④点E的坐标为(8,180).其中正确的有________________(填正确结论的序号).
参考答案:
【答案】①②④
【解析】①用540+300计算即可求解;
②根据速度=路程÷时间求出乙车的速度,速度和=路程和÷相遇时间求出两车的速度和,再相减即可求解;
③根据路程=速度×时间列式计算即可求解;
④根据点E的实际意义即两边第二次距B地路程相等列方程求解即可.
①540+300=840(千米),
故A、C之间的路程为840千米,正确;
②乙车的速度为:540÷6=90(千米/小时),
840÷5.6=150(千米/小时),
甲车的速度为:150-90=60(千米/小时),
90-60=30(千米/小时),
故乙车比甲车每小时快30千米,正确;
③840÷90=![]() (小时),
(小时),
![]() -300=260(千米)
-300=260(千米)
故当乙车到A点时,甲车距离B点250千米,错误;
④设当两车出发x小时后距B地的距离第二次相等,
![]() ,
,
解得,![]() ,
,
当![]() 时,
时,![]() ,
,
故点E的坐标为(8,180),正确,
故答案为:①②④.
-
科目: 来源: 题型:
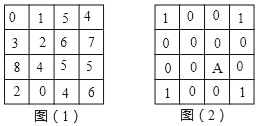
查看答案和解析>>【题目】在图(1)中,对任意相邻的上下或左右两格中的数字同时加1或减2,这算作一次操作,经过若干次操作后,图(1)能变为图(2),则图(2)中A格内的数是_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,抛物线
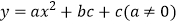 与
与 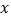 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 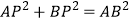 ,则称点P为抛物线
,则称点P为抛物线 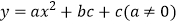 的勾股点。
的勾股点。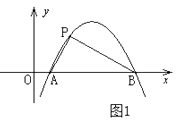
(1)直接写出抛物线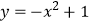 的勾股点的坐标;
的勾股点的坐标;
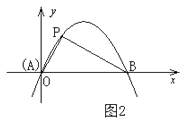
(2)如图2,已知抛物线C: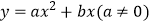 与
与 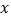 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, 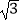 )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件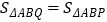 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】柯桥区某企业因为发展需要,从外地调运来一批94吨的原材料,现有甲、乙、丙三种车型共选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)若全部物资都用甲、乙两种车型来运送,需运费6400元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将-1、
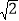 、
、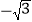 、2、
、2、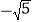 、
、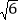 ……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.
……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.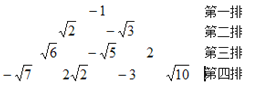
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:
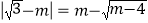 ,ABy轴于B,ACx轴于C
,ABy轴于B,ACx轴于C(1)求m的值;
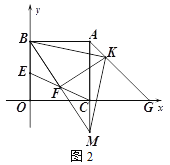
(2)如图1,BE=1,过A作AF⊥AE交x轴于F,连EF,D在AO上,且AD=AE,连接ED并延长交x轴于点P,求点P的坐标;
(3)如图2,G为线段OC延长线上一点,AC=CG,E为线段OB上一动点(不与O、B重合),F为线段CE的中点,若BF⊥FK交AG于K,延长BF、AC交于M,连接KM.请问∠FBK的大小是否变化?若不变,请求其值;若改变,求出变化的范围.

相关试题

