搜索
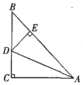
【题目】如图，△ABC中，∠C=90°,AC=BC，AD平分∠BAC, 点E正好在BD的垂直平分线上，且AB=6，则△DBE的周长是___________.
参考答案：
【答案】6
【解析】
根据角平分线上的点到角的两边距离相等可得CD=DE，然后利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AC=AE，再求出△DBE的周长=AB，从而得解．
解：∵∠C=90°，AD平分∠CAB，DE⊥AB，
∴CD=DE，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AC=AE，
∴△DBE的周长=DE+BD+BE，
=CD+BD+BE，
=BC+BE，
=AC+BE，
=AE+BE，
=AB，
∵AB=6，
∴△DBE的周长=6．
故答案为：6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:
因式分解的结果为
,当
时,
此时可以得到数字密码171920.(1)根据上述方法,当
时,对于多项式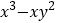
分解因式后可以形成哪些数字密码?(写出三个)(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式
分解因式后得到的密码(只需一个即可);(3)若多项式
因式分解后,利用本题的方法,当
时可以得到其中一个密码为242834,求m、n的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，∠B=90 ，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
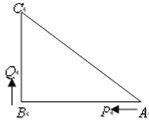
（1）出发2秒后，求PQ的长；
（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？
（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，CD、CM分别是斜边上的高和中线，那么下列结论中错误的是（ ）
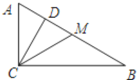
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=x2+bx+c的对称轴为x=2，且过点C（0，3）
（1）求此抛物线的解析式；
（2）证明：该抛物线恒在直线y=﹣2x+1上方．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,联结BD与CE交于点F，BD交AE于点G.
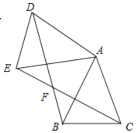
(1)求证:△AEC≌△ADB ;
(2)若AB=2,∠ACB=67.5°，AC∥DF ，求BD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D在Rt△ABC的斜边AB上，且AC=6,
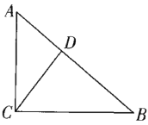
(1) 若AB比BC大2,①求AB的长；②若CD⊥AB于点D,求CD的长.
(2)若AD=7，DB=11， ∠CDB=2∠B，求CD的长.
相关试题
