【题目】某校为绿化校园,在一块长24米,宽19米的长方形空地的中央建造一个面积为300平方米的长方形花圃,要使四周留出一条宽相等的小路,可设小路宽为x,从而列出方程,求得小路的宽为________米.
参考答案:
【答案】(24-2x)(19-2x)=300
【解析】
可设小路宽为x,根据在一块长24米,宽19米的长方形空地的中央建造一个面积为300平方米的长方形花圃,要使四周留出一条宽相等的小路,可列出方程.
解:设小路宽为x,
(24-2x)(19-2x)=300.
故答案为:(24-2x)(19-2x)=300.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xn=2,yn=3,求(x2y)2n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
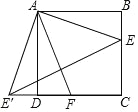
A.△AEE′是等腰直角三角形 B.AF垂直平分EE'
C.△E′EC∽△AFD D.△AE′F是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺为1:500000的地图上量得甲、乙两地的距离为4cm,则甲、乙两地的实际距离是___km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品原来每盒售价96元,由于两次降价,现在每盒售价54元,平均每次降价的百分率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列正多边形材料中,不能单独用来铺满地面的是( ).
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
相关试题

