【题目】提出问题:当x>0时如何求函数y=x+![]() 的最大值或最小值?
的最大值或最小值?
分析问题:前面我们刚刚学过二次函数的相关知识,知道求二次函数的最值时,我们可以利用它的图象进行猜想最值,或利用配方可以求出它的最值.
例如我们求函数y=x﹣2![]() (x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2
(x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2![]() =(
=(![]() )2﹣2
)2﹣2![]() ﹣2
﹣2![]() +1﹣1=(
+1﹣1=(![]() ﹣1)2﹣1即当x=1时,y有最小值为﹣1
﹣1)2﹣1即当x=1时,y有最小值为﹣1
解决问题
借鉴我们已有的研究函数的经验,探索函数y=x+![]() (x>0)的最大(小)值.
(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=x+![]() (x>0)的图象:
(x>0)的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |
(2)观察猜想:观察该函数的图象,猜想
当x= 时,函数y=x+![]() (x>0)有最 值(填“大”或“小”),是 .
(x>0)有最 值(填“大”或“小”),是 .
(3)推理论证:利用上述例题,请你尝试通过配方法求函数y=x+![]() (x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣
(x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣![]() (x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .
(x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .

参考答案:
【答案】(1)4![]() ;3
;3![]() ;2
;2![]() ;2;2
;2;2![]() ;3
;3![]() ;4
;4![]() ;画图见解析;(2)1,小,2;(3)
;画图见解析;(2)1,小,2;(3)![]() ,大,﹣2.
,大,﹣2.
【解析】
试题分析:(1)由x的值计算出y的值,填表即可;用描点法画出图象即可;
(2)用配方法得出y=x+![]() =(
=(![]() ﹣
﹣![]() )2+2,即可得出结果;
)2+2,即可得出结果;
(3)用配方法得出y=﹣2x﹣![]() =﹣(
=﹣(![]() ﹣
﹣![]() )2﹣2,即可得出结果.
)2﹣2,即可得出结果.
解:(1)当x=![]() 时,y=x+
时,y=x+![]() =
=![]() +4=4
+4=4![]() ;
;
当x=![]() 时,y=x+
时,y=x+![]() =
=![]() +3=3
+3=3![]() ;
;
当x=![]() 时,y=x+
时,y=x+![]() =
=![]() +2=2
+2=2![]() ;
;
当x=1时,y=x+![]() =1+1=2;
=1+1=2;
当x=2时,y=x+![]() =2+
=2+![]() =2
=2![]() ;
;
当x=3时,y=x+![]() =3+
=3+![]() =3
=3![]() ;
;
当x=4时,y=x+![]() =4+
=4+![]() =4
=4![]() ;填表如下:
;填表如下:
函数图象如图所示:
(2)∵y=x+![]() =(
=(![]() )2+(
)2+(![]() )2=(
)2=(![]() ﹣
﹣![]() )2+2,
)2+2,
∴当x=1时,函数y=x+![]() (x>0)有最小值,最小值为2;
(x>0)有最小值,最小值为2;
故答案为:1,小,2;
(3)∵y=﹣2x﹣![]() =﹣(2x+
=﹣(2x+![]() )=﹣(
)=﹣(![]() ﹣
﹣![]() )2﹣2,
)2﹣2,
∴当![]() =1,即x=
=1,即x=![]() 时,函数y=﹣2x﹣
时,函数y=﹣2x﹣![]() (x>0)有最大值,最大值为﹣2;
(x>0)有最大值,最大值为﹣2;
故答案为:![]() ,大,﹣2.
,大,﹣2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如果︱x+8︱=5,那么x=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=2(∠A+∠B),则∠C=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内有两点E、F满足AE=4,tanα=
 ,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为 .
,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为 .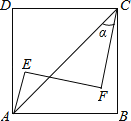
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
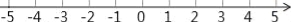
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在口ABCD中,AB⊥AC,AB=1,BC=
 ,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当旋转角为90时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知10箱苹果,以每箱15千克为标准,超过15的千克数记为正数,不足15的千克数记为负数,称重记录如下:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
(1)求10箱苹果的总重量;
(2)若每箱苹果的重量标准为15±0.5(千克),则这10箱中有几箱不符合标准的?
相关试题

