【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.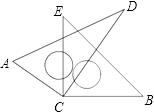
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
参考答案:
【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD
(2)解:由余角的定义,得∠ACE=90°﹣∠DCE=90°﹣30°=60°,
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°
(3)解:∠ACB+∠DCE=180°,理由如下:
由角的和差,得∠ACB=∠BCE+∠ACE,
∠ACB+∠DCE=∠BCE+(∠ACE+DCE)=∠BCE+∠ACE=180°
【解析】 (1)观察图形,根据同角的余角相等,可得出∠ACE+∠DCE=∠BCD+∠DCE=90°,可证得∠ACE=∠BCD。
(2) 根据余角的性质求出∠ACE的度数,再根据∠ACB=∠ACE+∠BCE,计算即可得出答案。
(3)根据图形易证∠ACB=∠BCE+∠ACE,而∠ACE+∠DCE=90°,就可证出∠ACB与∠DCE之和为180°。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数
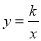 (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.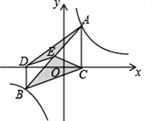
-
科目: 来源: 题型:
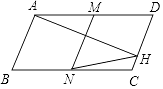
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,tan∠ACD=
 ,AB=5,那么CD的长是_____.
,AB=5,那么CD的长是_____.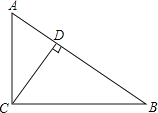
-
科目: 来源: 题型:
查看答案和解析>>【题目】变形与求值
(1)通分: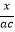 ,
,  .
.
(2)求值: ,其中x=1,y=﹣
,其中x=1,y=﹣  .
.
(3)不改变分式的值,变形使分式 的分子与分母的最高次项的系数是正数.
的分子与分母的最高次项的系数是正数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一人患了流感,经过两轮传染后共有64人患了流感,则每轮传染中平均一个人传染的人数是
A.5人B.6人C.7人D.8人
相关试题

