【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.

参考答案:
【答案】(1)![]() ;(2)S=﹣m2﹣4m,S的最大值为4.
;(2)S=﹣m2﹣4m,S的最大值为4.
【解析】试题分析:(1)根据抛物线与x轴的交点A与C坐标设出抛物线的二根式方程,将B坐标代入即可确定出解析式;
(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积﹣三角形AOB面积,求出即可.
试题解析:(1)设抛物线解析式为y=a(x+4)(x﹣2),将B(0,﹣4)代入得:﹣4=﹣8a,即a=![]() ,则抛物线解析式为y=
,则抛物线解析式为y=![]() (x+4)(x﹣2),即
(x+4)(x﹣2),即![]() ;
;
(2)过M作MN⊥x轴,将x=m代入抛物线得:y=![]() m2+m﹣4,即M(m,
m2+m﹣4,即M(m, ![]() m2+m﹣4),∴MN=|
m2+m﹣4),∴MN=|![]() m2+m﹣4|=﹣
m2+m﹣4|=﹣![]() m2﹣m+4,ON=﹣m,∵A(﹣4,0),B(0,﹣4),∴OA=OB=4,∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB=
m2﹣m+4,ON=﹣m,∵A(﹣4,0),B(0,﹣4),∴OA=OB=4,∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB=![]() ×(4+m)×(﹣
×(4+m)×(﹣![]() m2﹣m+4)+
m2﹣m+4)+![]() ×(﹣m)×(﹣
×(﹣m)×(﹣![]() m2﹣m+4+4)﹣
m2﹣m+4+4)﹣![]() ×4×4
×4×4
=2(﹣![]() m2﹣m+4)﹣2m﹣8
m2﹣m+4)﹣2m﹣8
=﹣m2﹣4m
=﹣(m+2)2+4
当m=﹣2时,S取得最大值,最大值为4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师带领学生到植物园参观,门票每张5元,购票才发现所带的钱不足,售票处工作人员告诉他:如果参观人数50人以上(含50人),可以按团体票享受8折优惠,于是王老师买了50张票,结果发现所带的钱还有剩余,那么王老师和他的学生至少有( )人.
A. 40 B. 41 C. 42 D. 43
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2(x﹣3)≤2a+1的自然数解只有0、1、2三个,则a的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有( )
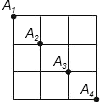
A. 4种 B. 6种 C. 8种 D. 10种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l是该轴对称图形的对称轴.

(1)试写出图中二组对应相等的线段: ;
(2)试写出二组对应相等的角: ;
(3)线段AB、CD都被直线l .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(1,a)和点N(2,b)是一次函数y=﹣2x+1图象上的两点,则a与b的大小关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.菱形的对角线互相平分B.顺次连接菱形各边中点得到的四边形是正方形
C.对角线相等的四边形是矩形D.顺次连接矩形各边中点得到的四边形是正方形
相关试题

