【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( ) 
A.45°
B.50°
C.55°
D.60°
参考答案:
【答案】A
【解析】解:∵四边形ABCD内接于⊙O,∠ABC=105°, ∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵ ![]() =
= ![]() ,∠BAC=30°,
,∠BAC=30°,
∴∠DCE=∠BAC=30°,
∴∠E=∠ADC﹣∠DCE=75°﹣30°=45°.
故选A.
【考点精析】通过灵活运用圆心角、弧、弦的关系和圆内接四边形的性质,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的两条对角线长分别是6cm和8cm,则菱形的边长是( )
A.5cm
B.7cm
C.10cm
D.12cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
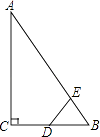
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.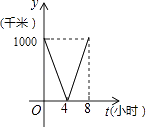
B.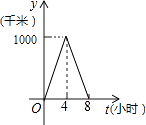
C.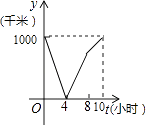
D.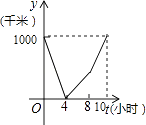
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
-
科目: 来源: 题型:
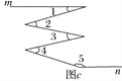
查看答案和解析>>【题目】如图,在图a、图b、图c中都有直线m∥n,
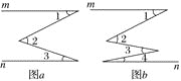
(1)在图a中,∠2和∠1、∠3之间的数量关系是__________________.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是____________________.
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,EF//AD,
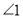 =
=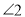 .求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
.求证:∠DGA+∠BAC=180°.请将说明过程填写完成.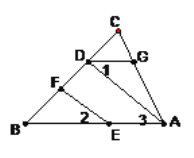
证明:∵EF//AD,(已知)
∴
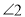 =_____(_____________________________).
=_____(_____________________________).又∵
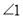 =
=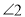 (______)
(______)∴
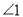 =
=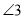 (________________________).
(________________________).∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
相关试题

