【题目】如图,△ABC,△CDE均为等边三角形(每个内角都是60°),连接BD,AE交于点O,BC与AE交于点P.试说明:∠POB=60°.经过观察分析,解题的关键是先利用( )说明△EAC≌△DBC.

A.SSSB.ASAC.SASD.AAS
参考答案:
【答案】C
【解析】
根据等边三角形的性质得到AC=PC,EC=EC,∠ACB=∠DCE=60°,得到∠ACE=∠BCD,再根据三角形全等的判定定理即可得到答案.
解:∵△ABC,△CDE均为等边三角形,
∴AC=PC,EC=EC,∠ACB=∠DCE=60°,
∴∠ACB+∠BCE=∠DCE+∠BCE,
即:∠ACE=∠BCD,
在△EAC和△DBC中,

∴△EAC≌△DBC(SAS),
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )

A.△ABC中,AB边上的高是CEB.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CED.△ACD中,CD边上的高是AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】从徐州到某地,若乘坐普通列车,行程为520km;若乘坐高铁,行程为400km.已知高铁的平均速度是普通列车的2.5倍,从徐州到该市乘坐高铁比乘坐普通列车少用3h.求高铁行驶的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2020,则至少需要操作__________次.

-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.

(1)如果用x(L)表示耗油量,用y(kg)表示开私家车的二氧化碳排放量,则y与x之间的关系式可表示为___________;
(2)在上述关系式中,耗油量每增加1L,二氧化碳排放量增加________kg.当耗油量从10L增加到100L时,二氧化碳排放量从________kg增加到________kg;
(3)小颖家本月家居用电的耗电量约为90kwh、开私家车的耗油量约为70L、天然气使用量约20m、自来水使用量约6吨,请你计算一下小颖家本月这几项的二氧化碳排放总量;
(4)你打算从哪些小事做起践行低碳生活?请直接写出两条.
-
科目: 来源: 题型:
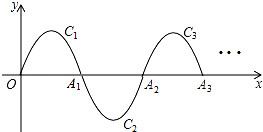
查看答案和解析>>【题目】如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 .
相关试题

