【题目】解下列方程:
(1)![]() .
.
(2)x2+4x﹣1=0.
参考答案:
【答案】
(1)解:去分母得:2x﹣4=3x﹣9,
解得:x=6,
经检验x=6是分式方程的解
(2)解:移项得:x2+4x=1,
配方得:x2+4x+4=5,即(x+2)2=5,
开方得:x+2=± ![]() ,
,
解得:x=﹣2± ![]() .
.
【解析】(1)根据解分式方程时必须要检验方程的解是原分式方程的解,还是增根,去分母得:2x﹣4=3x﹣9,解得x=6,经检验x=6是分式方程的解;(2)移项得:x2+4x=1,配方得:x2+4x+4=5,即(x+2)2=5,解得:x=﹣2± ![]() .
.
【考点精析】利用配方法和去分母法对题目进行判断即可得到答案,需要熟知左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某商品的原价为100元,连续两次涨价后的售价为144元,设两次平增长率为x.则下面所列方程正确的是( )
A.100(1﹣x)2=144
B.100(1+x)2=144
C.100(1﹣2x)2=144
D.100(1﹣x)2=144 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离
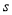 (千米)与时间
(千米)与时间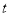 (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点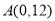 ,点
,点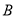 坐标为
坐标为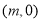 ,曲线
,曲线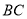 可用二次函数
可用二次函数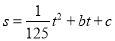 (
(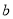 ,
,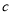 是常数)刻画.
是常数)刻画.(1)求
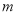 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以
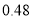 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为
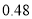 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度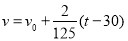 ,
,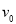 是加速前的速度).
是加速前的速度). -
科目: 来源: 题型:
查看答案和解析>>【题目】一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.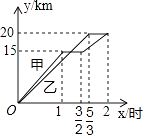
B.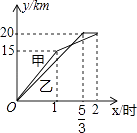
C.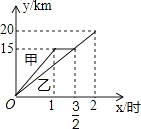
D.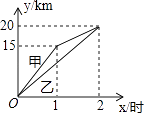
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一辆汽车以50 km/h的速度匀速行驶,行驶的路程为s(km),行驶的时间为t(h),则用t表示s的关系式为( )
A. s=50+50tB. s=50tC. s=50-50tD. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具厂计划加工3000套画图工具,为了尽快完成任务,实际每天加工画图工具的数量是原计划的1.2倍,结果提前4天完成任务,求该文具厂原计划每天加工这种画图工具的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一根弹簧长8 cm,它所挂物体的质量不能超过5 kg,并且所挂的物体每增加1 kg,弹簧就伸长0.5 cm,则挂上物体后弹簧的长度y(cm)与所挂物体的质量x(kg)(0≤x≤5)之间的关系式为( )
A. y=0.5(x+8)B. y=0.5x-8C. y=0.5(x-8)D. y=0.5x+8
相关试题

