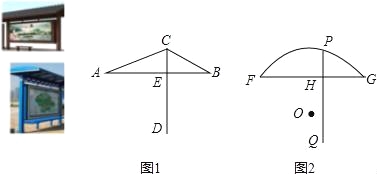
【题目】我市城市风貌提升工程正在火热进行中，检查中发现一些破旧的公交车候车亭有碍观瞻，现准备制作一批新的公交车候车亭，查看了网上的一些候车亭图片后，设计师画了两幅侧面示意图，AB，FG均为水平线段，CD⊥AB，PQ⊥FG，E，H为垂足，且AE=FH，AB=FG=2米，图1中tanA=，tanB=，图2点P在弧FG上．且弧FG所在圆的圆心O到FG，PQ的距离之比为5：2，

（1）求图1中的CE长；

（2）求图2中的PH长．

参考答案：

【答案】（1）0.48（2）0.6

【解析】

试题分析：（1）先根据已知条件得出AE=BE，再根据AE+BE=2，求得AE的长，最后计算CE的长即可；

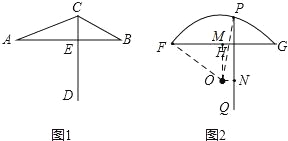
（2）先连接OF和OP，过点O作FG的垂线，作PQ的垂线，构造直角三角形，再根据勾股定理求得OF的长，进而得到OP长，最后根据勾股定理求得PN的长，进而利用线段的和差关系得到PH的长．

试题解析：（1）∵tanA==，tanB==

∴CE=AE，CE=BE

∴AE=BE

又∵AB=AE+BE=2

∴AE=1.2

∴CE=1.2×=0.48（m）

（2）过点O作FG的垂线，垂足为M，过点O作PQ的垂线，垂足为N，则

FM=1，MH=ON=1.2﹣1=0.2

∵O到FG，PQ的距离之比为5：2

∴OM=0.5=NH

连接OF和OP，则

直角三角形OFM中，OF==OP

∴直角三角形OPN中，PN==1.1

∴PH=PN﹣NH=1.1﹣0.5=0.6（m）

关闭