Question

【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

（2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标．

Answer 1

【答案】（1）y=x+3；y=-x2-2x+3，（2）M（-1，2）．

【解析】

试题分析：（1）根据题意得出关于a、b、c的方程组，求得a、b、c的值，即可得出抛物线的解析式，根据抛物线的对称性得出点B的坐标，再设出直线BC的解析式，把点B、C的坐标代入即可得出直线BC的解析式；

（2）点A关于对称轴的对称点为点B，连接BC，设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小，再求得点M的坐标．

试题解析：（1）依题意得：，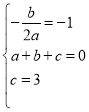

解之得：，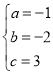

∴抛物线解析式为y=-x2-2x+3，

∵对称轴为x=-1，且抛物线经过A（1，0），

∴B（-3，0），

∴把B（-3，0）、C（0，3）分别代入直线y=mx+n，

得，

解得：，

∴直线y=mx+n的解析式为y=x+3；

（2）设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小．

把x=-1代入直线y=x+3得，y=2

∴M（-1，2）．

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（-1，2）．