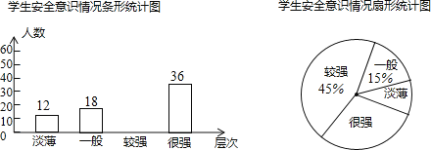
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
参考答案:
【答案】(1)120;(2)详见解析;(3)10%;108°.
【解析】
(1)根据安全意识一般的有18人,所占的百分比是15%,据此即可求得调查的总人数,再根据各层次人数之和等于总人数求得“较强”的人数及百分比的概念求得“很强、淡薄”的百分比可补全图形;
(2)总人数乘以“较强”和“很强”的百分比之和.
解:(1)调查的总人数是:18÷15%=120(人),;
(2)如图所示:
 ;
;
(3)安全意识为“淡薄”的学生占被调查学生总数的百分比=![]() =10%;
=10%;
安全意识为“很强”的学生所在扇形的圆心角的度数=![]() =108°
=108°
-
科目: 来源: 题型:
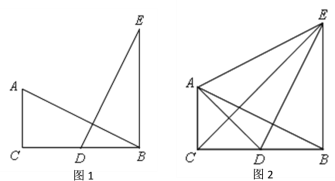
查看答案和解析>>【题目】如图,在
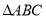 中,
中,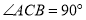 ,点
,点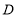 是直线
是直线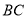 上一点.
上一点.
(1)如图1,若
 ,点
,点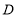 是
是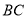 边的中点,点
边的中点,点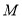 是线段
是线段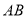 上一动点,求
上一动点,求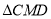 周长的最小值.
周长的最小值.(2)如图2,若
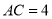 ,
,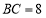 ,是否存在点
,是否存在点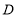 ,使以
,使以 ,
, ,
, 为顶点的三角形是等腰三角形,若存在,请直按写出线段
为顶点的三角形是等腰三角形,若存在,请直按写出线段 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由. -
科目: 来源: 题型:
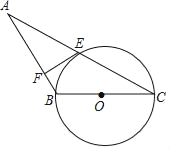
查看答案和解析>>【题目】如图所示,在△ABC中,AB=CB,以BC为直径的⊙O交AC于点E,过点E作⊙O的切线交AB于点F.
(1)求证:EF⊥AB;
(2)若AC=16,⊙O的半径是5,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C为线段OB的中点,D为线段OA上一点.连结AC、BD交于点P.
(问题引入)(1)如图1,若点P为AC的中点,求
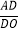 的值.
的值.温馨提示:过点C作CE∥AO交BD于点E.
(探索研究)(2)如图2,点D为OA上的任意一点(不与点A、O重合),求证:
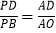 .
.(问题解决)(3)如图2,若AO=BO,AO⊥BO,
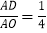 ,求tan∠BPC的值.
,求tan∠BPC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+3分别与x轴、y交于点B、C;抛物线y=x2+bx+c经过点B、C,与x轴的另一个交点为点A(点A在点B的左侧),对称轴为l1,顶点为D.
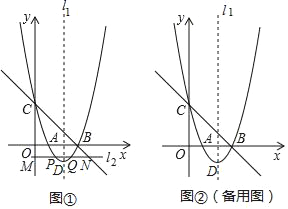
(1)求抛物线y=x2+bx+c的解析式.
(2)点M(0,m)为y轴上一动点,过点M作直线l2平行于x轴,与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3),且x2>x1>0.
①结合函数的图象,求x3的取值范围;
②若三个点P、Q、N中恰好有一点是其他两点所连线段的中点,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,AC=
 BC,点D为BC的中点,AB =DE,BE∥AC.
BC,点D为BC的中点,AB =DE,BE∥AC.(1)求证:△ABC≌△DEB;
(2)连结AD、AE、CE,如图2.
①求证:CE是∠ACB的角平分线;
②请判断△ABE是什么特殊形状的三角形,并说明理由.
相关试题

