【题目】【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形华为完全平方式或几个完全平方式的和,这种方法称之为配方法.例如:可将多项式![]() 通过恒等变形化为
通过恒等变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
【理解】对于多项式![]() ,当
,当![]() = 时,它的最小值为 .
= 时,它的最小值为 .
【应用】若![]() ,求
,求![]() 的值.
的值.
【拓展】![]() 、
、![]() 、
、![]() 是△
是△![]() 的三边,且有
的三边,且有![]() .
.
(1)若![]() 为整数,求
为整数,求![]() 的值.
的值.
(2)若△![]() 是等腰三角形,直接写出这个三角形的周长.
是等腰三角形,直接写出这个三角形的周长.
参考答案:
【答案】【理解】![]() ,
, ![]() ;【应用】
;【应用】![]() ;【拓展】(1)c的值为4,5,6;(2)12.
;【拓展】(1)c的值为4,5,6;(2)12.
【解析】【试题分析】
【理解】![]() =
=![]() ,得当
,得当![]() =2时,它的最小值为1.
=2时,它的最小值为1.
【应用】![]() ,
,
变形得: ![]() .
.
配方得: ![]() . 则
. 则![]() ,
, ![]() .解得
.解得![]() ,
, ![]() .
.
则![]() .
.
【拓展】
(1)![]() ,
, ![]() .
.
配方得: ![]() .则
.则![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
根据三角形两边之和大于第三边,两边之差小于第三边得: ![]() .
.
因为![]() 为整数,则
为整数,则![]() 的值为4,5,6
的值为4,5,6
(2)2,2,5(舍去)与5,5,2两种情况,得:等腰三角形的周长为12.
【试题解析】
【理解】![]()
![]()
【应用】∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
∴![]() .
.
【拓展】(1)∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
∴![]() .
.
∵![]() 为整数,
为整数,
∴![]() 的值为4,5,6.
的值为4,5,6.
(2)2,2,5(舍去)与5,5,2两种情况,得:等腰三角形的周长为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个同类项的和是( )
A. 单项式 B. 多项式
C. 可能是单项式也可能是多项式 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简
(1)﹣5m2n+4mn2﹣2mn+6m2n+3mn;
(2)2(2a﹣3b)﹣3(2b﹣3a). -
科目: 来源: 题型:
查看答案和解析>>【题目】如果A是3次多项式,B也是3次多项式, 那么A+B一定是( )
A. 6次多项式 B. 次数不低于3次的多项式
C. 3次多项式 D. 次数不高于3次的整式
-
科目: 来源: 题型:
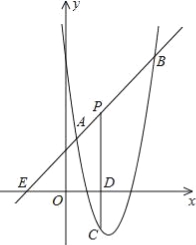
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=
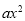 +bx+6(a≠0)相交于A(
+bx+6(a≠0)相交于A(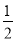 ,
,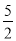 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x﹣3的顶点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中A(2,-3)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

