【题目】化简
(1)﹣5m2n+4mn2﹣2mn+6m2n+3mn;
(2)2(2a﹣3b)﹣3(2b﹣3a).
参考答案:
【答案】
(1)解:原式=(﹣5+6)m2n+4mn2﹣(2﹣3)mn
=m2n+4mn2+mn
(2)解:原式=4a﹣6b﹣6b+9a
=13a﹣12b
【解析】(1)直接合并同类项即可;(2)先去括号,再合并同类项即可.
【考点精析】通过灵活运用整式加减法则,掌握整式的运算法则:(1)去括号;(2)合并同类项即可以解答此题.
-
科目: 来源: 题型:
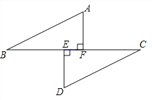
查看答案和解析>>【题目】如图,已知点
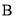 、
、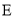 、
、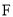 、
、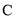 依次在同一条直线上,
依次在同一条直线上, 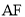 ⊥
⊥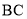 于点
于点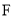 ,
, 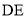 ⊥
⊥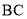 于点
于点 ,且
,且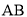 =
=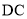 ,
, 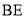 =
=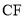 .
.(1)求证:
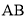 ∥
∥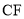 ;
;(2)连结
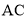 、
、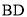 ,求证:
,求证: 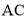 =
=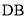 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=37°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个同类项的和是( )
A. 单项式 B. 多项式
C. 可能是单项式也可能是多项式 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A是3次多项式,B也是3次多项式, 那么A+B一定是( )
A. 6次多项式 B. 次数不低于3次的多项式
C. 3次多项式 D. 次数不高于3次的整式
-
科目: 来源: 题型:
查看答案和解析>>【题目】【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形华为完全平方式或几个完全平方式的和,这种方法称之为配方法.例如:可将多项式
 通过恒等变形化为
通过恒等变形化为 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.【理解】对于多项式
 ,当
,当 = 时,它的最小值为 .
= 时,它的最小值为 .【应用】若
 ,求
,求 的值.
的值.【拓展】
 、
、 、
、 是△
是△ 的三边,且有
的三边,且有 .
.(1)若
 为整数,求
为整数,求 的值.
的值.(2)若△
 是等腰三角形,直接写出这个三角形的周长.
是等腰三角形,直接写出这个三角形的周长. -
科目: 来源: 题型:
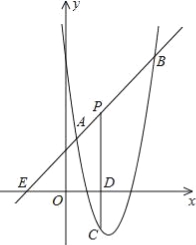
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=
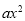 +bx+6(a≠0)相交于A(
+bx+6(a≠0)相交于A(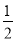 ,
,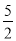 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
相关试题

