【题目】某超市第一次用4600元购进甲、乙两种商品,其中甲商品件数的2倍比乙商品件数的3倍少40件,甲、乙两种商品的进价和售价如下表(利润=售价﹣进价):
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 28 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多280元,则第二次乙商品是按原价打几折销售的?
参考答案:
【答案】(1)该超市第一次购进甲种商品100件,购进乙种商品80件;(2)(1400元;(3)九折.
【解析】
(1)设第一次购进甲种商品x件,购进乙种商品y件,根据题目中的等量关系列出方程组,求解即可.
(2)根据利润=售价-进价,再乘以销售量即可求出购进的甲、乙两种商品全部卖出后一共可获得利润.
(3)设第二次乙种商品是按原价打m折销售的,根据等量关系列出方程,求解即可.
解:(1)设第一次购进甲种商品x件,购进乙种商品y件,
根据题意得:![]()
解得![]()
答:该超市第一次购进甲种商品100件,购进乙种商品80件.
(2)(28﹣22)×100+(40﹣30)×80=1400(元).
答:该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得1400元.
(3)设第二次乙种商品是按原价打m折销售的,
根据题意得:
![]()
解得:m=9.
答:第二次乙商品是按原价打九折销售.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:|﹣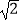 |+(
|+(  )﹣1﹣2cos45°.
)﹣1﹣2cos45°.
(2)解方程: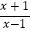 +
+ 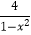 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器公司计划装运甲、乙、丙三种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电).下表所示为装运甲、乙、丙三种家电的台数及利润.
甲
乙
丙
每辆汽车能装运的台数
40
20
30
每台家电可获利润(万元)
0.05
0.07
0.04
(1)若用8辆汽车装运乙、丙两种家电190台到A地销售,问装运乙、丙的汽车各多少辆.
(2)计划用20辆汽车装运甲、乙、丙三种家电720台到B地销售,如何安排装运,可使公司获得36.6万元的利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥CD,∠BED=90°.填空:
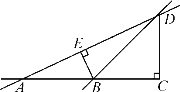
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
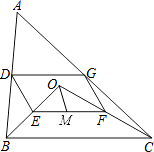
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图所示,O是直线AB上一点,∠AOC=
 ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
相关试题

