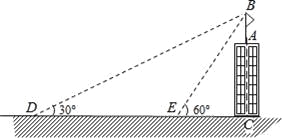
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
参考答案:
【答案】约是5.3米.
【解析】试题分析:由条件可知BE=DE=20米,再在Rt△BCE中,利用三角函数可求得BC的长,进而可求得AB的长.
试题解析:∵∠BEC=∠BDE+∠DBE,∴∠DBE=∠BEC-∠BDC=60°-30°=30°,∴∠BDE=∠DBE,∴BE=DE=20米.在Rt△BCE中,∠BCE=90°,sin∠BEC=![]() ,∴
,∴![]() (米),∴AB=BC-AC=17.3-12=5.3(米).答:旗杆AB的高度为5.3米.
(米),∴AB=BC-AC=17.3-12=5.3(米).答:旗杆AB的高度为5.3米.
-
科目: 来源: 题型:
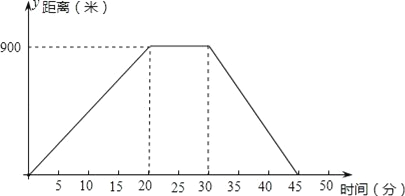
查看答案和解析>>【题目】如图所示,是反映了爷爷每天晚饭或从家中出发去散步的时间与距离之间的关系的一幅图.
(1)下图反映了哪两个变量之间的关系?
(2)爷爷从家里出发后20分钟到30分钟可能在做什么?
(3)爷爷每天散步多长时间?
(4)爷爷散步时最远离家多少米?
(5)计算爷爷离开家后的20分钟内的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3x=0的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x满足(x2-x)2-4(x2-x)-5=0,则x2-x的值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P(1,﹣4)、Q(m,n)在函数
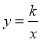 (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )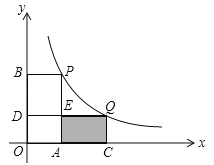
A.减小 B.增大 C.先减小后增大 D.先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】对角线互相的平行四边形是菱形.
相关试题

