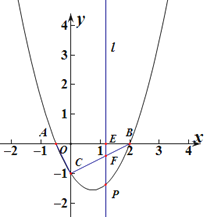
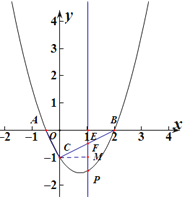
【题目】如图,二次函数 ![]() 的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
(1)求二次函数解析式;
(2)直线![]() 与
与![]() 轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
①求线段PF取得最大值时,OE的长;
②四边形ACPB的面积是否存在最大值?如果存在求出此最大值和点P的坐标;如果不存在,说明理由.
(3)不解方程组,直接写出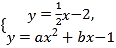 的解.
的解.
参考答案:
【答案】(1)![]() (2)①1;
(2)①1; ![]() (3)
(3)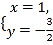
【解析】分析:(1)由△AOC∽△COB得:OA=![]() ,则点A(-
,则点A(-![]() ,0),把A、B代入联立方程组,即可求解;(2)①由题意得到直线BC的解析式为:
,0),把A、B代入联立方程组,即可求解;(2)①由题意得到直线BC的解析式为: ![]() ,分别设出点E、F、P的坐标,用含m的式子表示,从而求出线段PF取得最大值时,OE的长;
,分别设出点E、F、P的坐标,用含m的式子表示,从而求出线段PF取得最大值时,OE的长;
②利用![]() ,得到关于m的二次函数,配成顶点式,即可求解;(4)根据函数图象可得出结果.
,得到关于m的二次函数,配成顶点式,即可求解;(4)根据函数图象可得出结果.
本题解析:
(1)∵∠ACB=90o, ![]() ,∴
,∴![]()
∴![]() ,∴点A的坐标为
,∴点A的坐标为![]()
∴ ∴
∴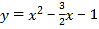
∴![]()
(2)①设直线BC的解析式为![]() ,由图象得:
,由图象得:
![]() , ∴
, ∴![]()
∴直线BC的解析式为: ![]() .
.
如图,设:E![]() ,则F
,则F![]() ,p
,p![]() ,
,
∴当m=1时, ![]()
∴OE=1
② 如图:
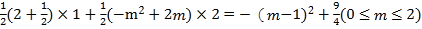
四边形ACPB的面积存在最大值,
![]()
=![]() ,
,
![]() ,
,
∴P(1, ![]() ).
).
(3)由图可知:

方程组: 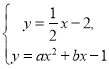 的解为
的解为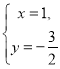
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3sB.4sC.5sD.6s
-
科目: 来源: 题型:
查看答案和解析>>【题目】温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地
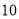 台,杭州厂可支援外地
台,杭州厂可支援外地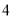 台.现在决定给武汉
台.现在决定给武汉 台,南昌
台,南昌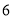 台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为
台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为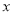 台.
台.南昌
武汉
温州厂
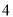
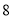
杭州厂
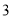
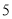
(
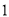 )用
)用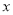 的代数式来表示总运费(单位:百元).
的代数式来表示总运费(单位:百元).(
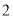 )若总运费为
)若总运费为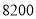 元,则杭州运往南昌的机器应为多少台?
元,则杭州运往南昌的机器应为多少台?(
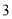 )试问有无可能使总运费是
)试问有无可能使总运费是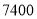 元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
元?若有可能,请写出相应的调运方案;若无可能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】点M在一次函数y=2x﹣1的图象上,则M的坐标可能为( )
A. (1,1) B. (1,﹣1) C. (﹣2,0) D. (2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种传染病,若有一人感染,经过两轮传染后将共有49人感染.设这种传染病每轮传染中平均一个人传染了x个人,列出方程为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的两项,属于同类项的是( )
A. ﹣2x2y与xy2B. 5x2y与﹣0.5x2z
C. 3mn与﹣4nmD. ﹣0.5ab与abc
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸距出发地1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
(1)图中
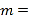 ,
, 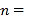 ;
;(2)求小明和爸爸相遇的时间.
相关试题

