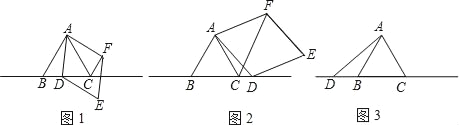
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,
①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.
参考答案:
【答案】(1)①详见解析;②∠AFC=∠ACB+∠DAC成立;(2)结论∠AFC=∠ACB+∠DAC不成立,理由详见解析;(3)图详见解析,∠AFC=2∠ACB﹣∠DAC.
【解析】
(1)此题只需由AB=AC,AD=AF,∠BAD=∠CAF,按照SAS判断两三角形全等得出∠ADB=∠AFC;
(2)此题应先判断得出正确的等量关系,然后再根据△ABD≌△ACF即可证明;
(3)此题只需补全图形后由图形即可得出∠AFC、∠ACB、∠DAC之间存在的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:关于x的二次函数
 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔一名选手参加“美丽运城,我为家乡做代言”主题演讲比赛,经研究,按如图所示的项目和权数对选拔赛的参赛选手进行考评(因排版原因统计图不完整).
下表是李明、张华在选拔赛中的得分情况:
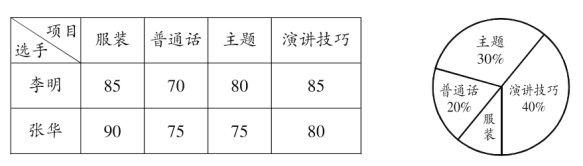
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽运城,我为家乡做代言”主题演讲比赛,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

-
科目: 来源: 题型:
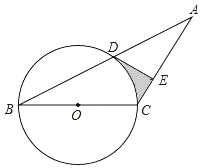
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求阴影部分的面积.
相关试题

