【题目】已知关于 ![]() 的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
(1)求实数 m 的取值范围;
(2)当 x12-x22 时,求 m 的值.
参考答案:
【答案】
(1)解:因为一元二次方程x2+(2m-1)x+m2=0有两个实数根,
∴△= b2-4ac=(2m-1)2-4×1×m2=-4m+1≥0,
∴m≤ ![]() ,
,
即实数m的取值范围为m≤ ![]()
(2)解:当x12-x22=0时,即(x1+x2)(x1-x2)=0,∴x1+x2=0或x1-x2=0,当x1+x2=0,依据一元二次方程根与系数的关系可得x1+x2=-(2m-1),∴-(2m-1)=0,∴m= ![]() ,又∵由(1)一元二次方程x2+(2m-1)x+m2=0有两个实数根时的取值范围是m≤
,又∵由(1)一元二次方程x2+(2m-1)x+m2=0有两个实数根时的取值范围是m≤ ![]() ,∴m=
,∴m= ![]() 不成立,故m无解;当x1-x2=0时,x1=x2,方程有两个相等的实数根, ∴△=(2m-1)2-4×1×m2=-4m+1=0,∴m=
不成立,故m无解;当x1-x2=0时,x1=x2,方程有两个相等的实数根, ∴△=(2m-1)2-4×1×m2=-4m+1=0,∴m= ![]() ,综上所述,当x12-x22=0时,m=
,综上所述,当x12-x22=0时,m= ![]()
【解析】(1)根据题意可知,方程有两个实数根,则 b2-4ac≥0,建立不等式求解即可。
(2)将x12-x22=0变形为(x1+x2)(x1-x2)=0,在m取值范围为m≤ ![]() 时,分情况讨论:当x1+x2=0;x1-x2=0时,求出符合条件的m的值。
时,分情况讨论:当x1+x2=0;x1-x2=0时,求出符合条件的m的值。
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=2∠C,AD⊥BC于D,设AD=b,BD=a,则DC=_____.(用含a,b的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填出下表:
剪的次数
1
2
3
4
5
6
正方形个数
(2)如果剪了100次,共剪出 个小正方形?
(3)如果剪
 次,共剪出 个小正方形?
次,共剪出 个小正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了调查八年级学生参加“乒乓”、“篮球”、“足球”、“排球”四项体育活动的人数,学校从八年级随机抽取了部分学生进行调查,根据调查结果制作了如下不完整的统计表、统计图:


请你根据以上信息解答下列各题:
(1)a= ;b= ;c= ;
(2)在扇形统计图中,排球所对应的圆心角是 度;
(3)若该校八年级共有600名学生,试估计该校八年级喜欢足球的人数?
-
科目: 来源: 题型:
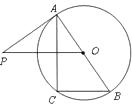
查看答案和解析>>【题目】如图,已知
 是
是 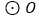 的直径,过点
的直径,过点 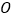 作弦
作弦 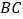 的平行线,交过点
的平行线,交过点 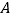 的切线
的切线 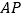 于点
于点 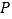 ,连结
,连结 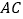 .
.
(1)求证: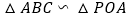 ;
;
(2)若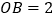 ,
, 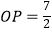 ,求
,求 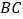 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.

(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
相关试题

