【题目】如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( ) 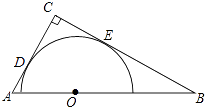
A.2.5
B.1.6
C.1.5
D.1
参考答案:
【答案】B
【解析】解:连接OD、OE, 设AD=x,
∵半圆分别与AC、BC相切,
∴∠CDO=∠CEO=90°,
∵∠C=90°,
∴四边形ODCE是矩形,
∴OD=CE,OE=CD,
又∵OD=OE,
∴CD=CE=4﹣x,BE=6﹣(4﹣x)=x+2,
∵∠AOD+∠A=90°,∠AOD+∠BOE=90°,
∴∠A=∠BOE,
∴△AOD∽OBE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=1.6,
故选:B.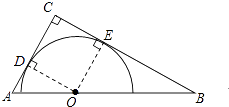
【考点精析】通过灵活运用切线的性质定理和相似三角形的判定与性质,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
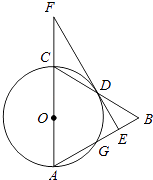
(1)求证:直线EF是⊙O的切线;
(2)若CF=5,cosA=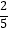 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.

(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由. -
科目: 来源: 题型:
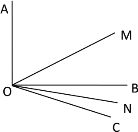
查看答案和解析>>【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)若题干中的∠AOB=
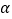 ,其他条件不变,求∠MON的度数;
,其他条件不变,求∠MON的度数;(3)若题干中的∠BOC=
 (
( 为锐角),其他条件不变,求∠MON的度数;
为锐角),其他条件不变,求∠MON的度数;(4)综合(1)(2)(3)的结果,你能得出什么结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市实行阶梯电价制度,居民家庭每月用电量不超过80千瓦时时,实行“基本电价”;当每月用电量超过80千瓦时时,超过部分实行“提高电价”.去年小张家4月用电量为100千瓦时,交电费68元;5月用电量为120千瓦时,交电费88元.则基本电价”是__元/千瓦时,“提高电价”是__元/千瓦时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某工厂通过科技创新,生产效率不断提高.已知去年月平均生产量为120台机器,今年一月份的生产量比去年月平均生产量增长了m%,二月份的生产量又比一月份生产量多50台机器,而且二月份生产60台机器所需要时间与一月份生产45台机器所需时间相同,三月份的生产量恰好是去年月平均生产量的2倍.
问:今年第一季度生产总量是多少台机器?m的值是多少?
相关试题

