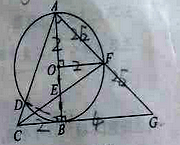
【题目】(2016山东省聊城市第24题)如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、DC=![]()
【解析】
试题分析:(1)、直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;(2)、首选得出△FOE≌△CBE(ASA),则BC=FO=![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
试题解析:(1)、∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在![]() 的中点, ∴
的中点, ∴![]() =
=![]() ,
,
∴∠AOF=∠BOF, ∵∠ABC=∠ABG=90°, ∴∠AOF=∠ABG, ∴FO∥BG, ∵AO=BO,
∴FO是△ABG的中位线, ∴FO=![]() BG;
BG;
(2)、在△FOE和△CBE中, , ∴△FOE≌△CBE(ASA), ∴BC=FO=
, ∴△FOE≌△CBE(ASA), ∴BC=FO=![]() AB=2,
AB=2,
∴AC=![]() =2
=2![]() , 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
, 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
∵∠BCD=∠ACB, ∴△BCD∽△ACB, ∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得:DC=
, 解得:DC=![]() .
.
-
科目: 来源: 题型:
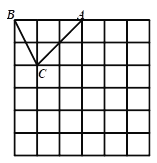
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列调查中,适宜采用全面调查的是( )
A. 了解明德集团所有中学生的视力情况
B. 了解某校七(4)班学生校服的尺码情况
C. 调查北京2017年的游客流量
D. 调查中国“2018俄罗斯世界杯”栏目的收视率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b(k≠0)的图象与x轴交于(﹣5,0),则关于x的一元一次方程kx+b=0的解为_____.
-
科目: 来源: 题型:
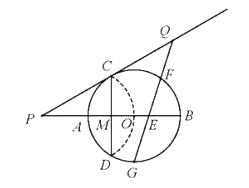
查看答案和解析>>【题目】(2016广东省深圳市第22题)如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
-
科目: 来源: 题型:
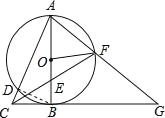
查看答案和解析>>【题目】(2016浙江省温州市第21题)如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F.
(2)若sinB=
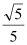 ,EF=2
,EF=2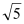 ,求CD的长.
,求CD的长.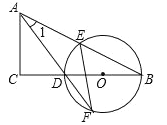
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

相关试题

