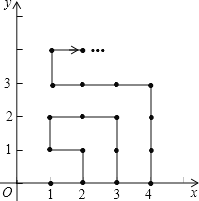
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
参考答案:
【答案】![]()
【解析】
根据点的坐标的变化可得出“第(2n1)2个点的坐标为(2n1,0)(n为正整数)”,依此规律可得出第2025个点的坐标为(45,0),再结合第2019个点在第2025个点的上方6个单位长度处,即可求出第2019个点的坐标,此题得解.
解:观察图形,可知:第1个点的坐标为(1,0),第4个点的坐标为(1,1),第9个点的坐标为(3,0),第16个点的坐标为(1,3),…,
∴第(2n1)2个点的坐标为(2n1,0)(n为正整数).
∵2025=452,
∴第2025个点的坐标为(45,0).
又∵20256=2019,
∴第2019个点在第2025个点的上方6个单位长度处,
∴第2019个点的坐标为(45,6).
故答案为:(45,6).
-
科目: 来源: 题型:
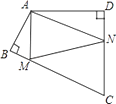
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD= 120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
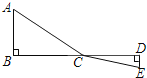
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式
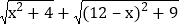 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BC=8,∠BAC=120°,作AD⊥BC于点D,AD=
 AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.
AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:我们学过一次函数的图象的平移,如:将一次函数
 的图象沿x轴向右平移1个单位长度可得到函数
的图象沿x轴向右平移1个单位长度可得到函数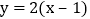 的图象,再沿y轴向上平移1个单位长度,得到函数
的图象,再沿y轴向上平移1个单位长度,得到函数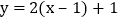 的图象;如果将一次函数
的图象;如果将一次函数 的图象沿x轴向左平移1个单位长度可得到函数
的图象沿x轴向左平移1个单位长度可得到函数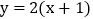 的图象,再沿y轴向下平移1个单位长度,得到函数
的图象,再沿y轴向下平移1个单位长度,得到函数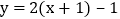 的图象;仿照上述平移的规律,解决下列问题:
的图象;仿照上述平移的规律,解决下列问题: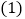 将一次函数
将一次函数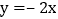 的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;
的图象沿x轴向右平移3个单位长度,再沿y轴向上平移1个单位长度,得到函数的图象;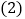 将
将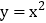 的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象;
的函数图象沿y轴向下平移3个单位长度,得到函数的图象,再沿x轴向左平移1个单位长度,得到函数的图象; 函数
函数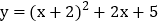 的图象可由
的图象可由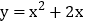 的图象经过怎样的平移变换得到?
的图象经过怎样的平移变换得到? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是多少?
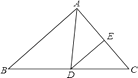
-
科目: 来源: 题型:
查看答案和解析>>【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果
芦柑
香梨
每辆汽车载货量
 吨
吨
7
6
5
每车水果获利
 元
元
2500
3000
2000
 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
相关试题

