【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
参考答案:
【答案】①、②、③、④.
【解析】试题分析:①∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B∴∠ADE=∠C,∴△ADE∽△ACD;故①正确,
②AB=AC=10,∠ADE=∠B=α,cosα=![]() ,∴BC=2ABcosB=2×10×
,∴BC=2ABcosB=2×10×![]() =16,∵BD=6,∴DC=10,∴AB=DC,
=16,∵BD=6,∴DC=10,∴AB=DC,
在△ABD与△DCE中,∠BAD=∠CDE ∠B=∠C AB=DC ∴△ABD≌△DCE(ASA). 故②正确,
③当∠AED=90°时,由①可知:△ADE∽△ACD,∴∠ADC=∠AED,∵∠AED=90°,∴∠ADC=90°,即AD⊥BC,
∵AB=AC,∴BD=CD,∴∠ADE=∠B=α且cosα=![]() ,AB=10,BD=8.
,AB=10,BD=8.
当∠CDE=90°时,易△CDE∽△BAD,∵∠CDE=90°,∴∠BAD=90°,∵∠B=α且cosα=![]() .AB=10,
.AB=10,
∴cosB=![]() =
=![]() ∴BD=
∴BD=![]() . 故③错误.
. 故③错误.
④易证得△CDE∽△BAD,由②可知BC=16,设BD=y,CE=x,∴![]() ∴
∴![]()
整理得: ![]() -16y+64=64-10x, 即
-16y+64=64-10x, 即![]() =64-10x, ∴0<x≤6.4. 故④正确.
=64-10x, ∴0<x≤6.4. 故④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣6=0时,原方程应变形为( )
A.(x+1)2=7
B.(x﹣1)2=7
C.(x+2)2=10
D.(x﹣2)2=10 -
科目: 来源: 题型:
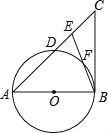
查看答案和解析>>【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=50°.
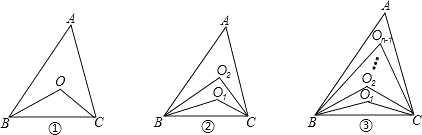
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC= °.
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (a3)3=a6B. a6÷a2=a3C. a5+a3=a8D. aa3=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各角能成为某多边形的内角和是( )
A. 4300° B. 4343° C. 4320° D. 4360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:﹣3a2+12=_____.
相关试题

