【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC
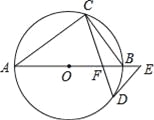
(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)详见解析;(2)5.
【解析】试题分析:(1)连接OD,由AB是⊙O的直径可得∠ACB=90°,所以∠A+∠ABC=90°,即可证得∠BOD=∠A,从而推出∠ODE=90°,即可得到结论;(2)连接BD,过D作DH⊥BF于H,由弦切角定理得到∠BDE=∠BCD,推出△ACF与△FDB都是等腰三角形,根据等腰直角三角形的性质得到FH=BH=![]() BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠BOD=2∠BCD,∠A=2∠BCD,
∴∠BOD=∠A,
∵∠AED=∠ABC,
∴∠BOD+∠AED=90°,
∴∠ODE=90°,
即OD⊥DE,
∴DE与⊙O相切;
(2)解:连接BD,过D作DH⊥BF于H,
∵DE与⊙O相切,
∴∠BDE=∠BCD,
∵∠AED=∠ABC,
∴∠AFC=∠DBF,
∵∠AFC=∠DFB,
∴△ACF与△FDB都是等腰三角形,
∴FH=BH=![]() BF=1,则FH=1,由勾股定理可得HD==3,
BF=1,则FH=1,由勾股定理可得HD==3,
在Rt△ODH中,OH2+DH2=OD2,
即(OD﹣1)2+32=OD2,
∴OD=5,
∴⊙O的半径是5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+
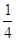 与y轴相交于点A,点B与点O关于点A对称
与y轴相交于点A,点B与点O关于点A对称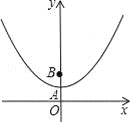
(1)填空:点B的坐标是 ;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;
(3)在(2)的条件下,若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上,求此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则b2﹣4ac满足的条件是( )
A. b2﹣4ac=0 B. b2﹣4ac>0 C. b2﹣4ac<0 D. b2﹣4ac≥0
-
科目: 来源: 题型:
查看答案和解析>>【题目】鸡兔同笼,数头有8只,数脚有26只,笼中有________只鸡,________只兔.
-
科目: 来源: 题型:
查看答案和解析>>【题目】垂直于同一条直线的两直线平行.________.(填“对'或'错”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线m外有一定点A,A到直线m的距离是7 cm,B是直线m上的任意一点,则线段AB的长度:AB___________7 cm.(填写“<”“>”“=”“≤”或“≥”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形、直角三角形、等边三角形、长方形、圆和扇形中,一定是轴对称图形的有( )
A. 6个 B. 5个 C. 4个 D. 3个
相关试题

