【题目】综合题
(1)已知 ![]() 是有理数且满足:
是有理数且满足: ![]() 是-27的立方根,
是-27的立方根, ![]() ,求
,求 ![]() 的值;
的值;
(2)已知 ![]() ,求
,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)解:∵a是-27的立方根,
∴a=-3,
∵ ![]() =7,
=7,
∴b=±7,
∴a2+2b=23或-5
(2)解:∵a-b=2,a-c= ![]() ,
,
∴b-c=- ![]() ,
,
∴b-c+ ![]() =0,
=0,
∴原式=(b-c+ ![]() )2=0
)2=0
【解析】(1)根据立方根和算术平方根的定义求出a、b的值,再将a、b的值代入代数式计算即可得出答案。
(2)根据已知a-b、a-c的值消去a,求出b-c的值,再整体代入求值即可。
【考点精析】解答此题的关键在于理解算数平方根的相关知识,掌握正数a的正的平方根叫做a的算术平方根;正数和零的算术平方根都只有一个,零的算术平方根是零,以及对立方根的理解,了解如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根);一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:四边形ABCD中,AB=CB=
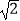 ,CD=
,CD= 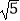 ,DA=1,且AB⊥CB于B.
,DA=1,且AB⊥CB于B.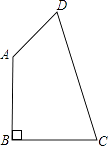
试求:
(1)∠BAD的度数;
(2)四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或︱m-n︱.利用数形结合思想解决下列问题:
已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)点A表示的数为 , 点B表示的数为 , 点C表示的数为 .
(2)用含t的代数式表示P到点A和点C的距离: PA= , PC= .
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动, Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2×3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “农民也可以报销医疗费了!”这是某市推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.
根据以上信息,解答以下问题:
(1)本次调查了多少村民,被调查的村民中,有多少人参加合作医疗得到了返回款;
(2)该乡若有10 000村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9 680人,假设这两年的年增长率相同,求这个年增长率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=
 x的图象与一次函数y=kx﹣3的图象相交于点(2,a).
x的图象与一次函数y=kx﹣3的图象相交于点(2,a). 
(1)求a的值.
(2)求一次函数的表达式.
(3)在同一坐标系中,画出这两个函数的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是30cm,则线段MN的长是 .

相关试题

