【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
(1)求证: ![]() .
.
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即
![]() ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= ________,T(120°)=_________,若α是等腰三角形的顶角,则T(α)的取值范围是_____________________;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点这沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
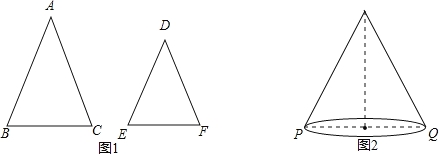
参考答案:
【答案】 ![]()
![]() 0<T(α)<2
0<T(α)<2
【解析】试题分析:(1)证明△ABC∽△DEF,根据相似三角形的性质解答即可;
(2)①根据等腰直角三角形的性质和等腰三角形的性质进行计算即可;
②根据圆锥的侧面展开图的知识和扇形的弧长公式计算,得到扇形的圆心角,根据T(A)的定义解答即可.
(1)∵AB=AC,DE=DF,∴ ![]() ,又∵∠A=∠D,∴△ABC∽△DEF,∴
,又∵∠A=∠D,∴△ABC∽△DEF,∴![]() ;
;
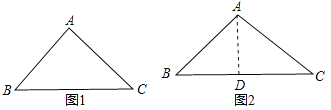
(2)①如图1,∠A=90°,AB=AC,则![]() =
=![]() ,∴T(90°)=
,∴T(90°)=![]() ,如图2,∠A=90°,AB=AC,作AD⊥BC于D,则∠B=60°,∴BD=
,如图2,∠A=90°,AB=AC,作AD⊥BC于D,则∠B=60°,∴BD=![]() AB,∴BC=
AB,∴BC=![]() AB,∴T(120°)=
AB,∴T(120°)=![]() ;
;
∵AB﹣AC<BC<AB+AC,∴0<T(α)<2,故答案为: ![]() ;
; ![]() ;0<T(α)<2;
;0<T(α)<2;
②∵圆锥的底面直径PQ=8,∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,设扇形的圆心角为n°,则![]() =8π,解得,n=160,∵T(80°)≈1.29,∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
=8π,解得,n=160,∵T(80°)≈1.29,∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a﹣2|和(b+5)2互为相反数,则a+b的值为( )
A.3
B.﹣3
C.7
D.﹣7 -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲处工作的有232人,在乙处工作的有146人,如果从乙处调x人到甲处,那么甲处工作的人数是乙处工作人数的3倍,则下列方程中,正确的是( )
A.3(323+x)=146﹣x
B.232﹣x=3(146﹣x)
C.232+x=3×146﹣x
D.232+x=3(146﹣x) -
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个比﹣2小的有理数 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在向学生调查“我最喜爱的科目”时,向学生询问以下几个问题,不合理的是( )
①你喜欢上的课是什么课?②你比较喜欢的科目是什么?③你喜欢上学吗?
A. ① B. ①② C. ② D. ③
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品按进价加20%作为定价,总卖不出去,后来老板按定价减价20%,以96元卖出,则这次生意(填“赚或赔多少元”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2-x-(m+1)=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为符合条件的最小整数,求此方程的根.
相关试题

