【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
参考答案:
【答案】设每年市政府投资的增长率为x, ……………1分
根据题意,得:2+2(1+x)+2(1+x)2=9.5, ……………2分
整理,得:x2+3x-1.75=0, ……………3分
解之,得:x=![]() ,
,
∴x1="0.5 " x2=-0.35(舍去) ……………5分
答:每年市政府投资的增长率为50%; ……………6分
(2)到2012年底共建廉租房面积=9.5÷![]() (万平方米).…………8分
(万平方米).…………8分
【解析】试题分析:(1)设每年市政府投资的增长率为x.根据到2016年底三年共累计投资9.5亿元人民币建设廉租房,列方程求解;
(2)先求出单位面积所需资金,再用累计投资÷单位面积所需钱数可得结果.
试题解析:(1)设每年市政府投资的增长率为x
则2015年投入的资金为![]() 亿元,2016年投入的资金为
亿元,2016年投入的资金为![]() 亿元,
亿元,
依题意,得 ![]() ;
;
解得:x1=0.5, x2=-3.5(不合题意,舍去).
答:每年市政府投资的增长率为50%;
(2)依题意,得3年的建筑面积共为:9.5÷(2÷8)=38(万平方米)
答:到2016年底共建设了38万平方米的廉租房.
点睛:此题主要考查了一元二次方程得应用,根据题意正确表示出每年的投资金额是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )

A.6cm2B.8 cm2C.10 cm2D.12 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+(m+2)x+2m-1=0.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,点D的坐标是(0,
 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,求证四边形AGBD是矩形.

-
科目: 来源: 题型:
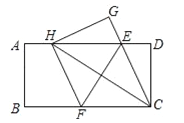
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②线段BF的取值范围为3≤BF≤4;
③EC平分∠DCH;④当点H与点A重合时,EF=
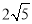 .
.以上结论中,你认为正确的有______.(填序号)
相关试题

