【题目】已知矩形ABCD,点P为边BC上一动点,连接AP,将线段AP绕点P顺时针旋转90°,点A恰好落在直线CD上点E处
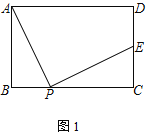
(1) 如图1,点E在线段CD上,求证:AD+DE=2AB
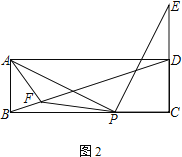
(2) 如图2,点E在线段CD的延长线上,且点D 为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB,求证:∠APF=∠ADB
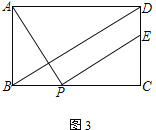
(3) 如图3,点E在线段CD上,连接BD.若AB=2,BD∥PE,则DE=___________ (直接写出结果)
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】试题分析:(1)用同角的余角相等得出∠BAP=∠CPE,进而判断出△ABP≌△PCE,即可的得出AB=PC=CD,BP=CE,最后用相等的线段代换即可;
(2)先判断出四边形ABDE是平行四边形则有BD∥AE,即可得到, ![]() 再判断出,△APF≌△EPD,则有∠AFP=∠DEP,最后用三角形的外角和等角代换即可;
再判断出,△APF≌△EPD,则有∠AFP=∠DEP,最后用三角形的外角和等角代换即可;
(3)先借助(1)的结论得出PC=AB=2, AD=4DE,再判断出△CPE∽△CBD,则有![]() 最后代值解关于
最后代值解关于![]() 的方程即可.
的方程即可.
试题解析:(1)∵四边形ABCD是矩形,
∴![]()
∴![]()
∵![]()
∴![]()
∴∠BAP=∠CPE,
在△ABP和△PCE中, 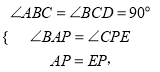
∴△ABP≌△PCE,
∴AB=PC=CD,BP=CE,
∴AD+DE=BC+DE=BP+PC+DE=CE+CP+DE=CP+CD=2AB;
(2)如图,
∵AB=AF,
∴∠ABF=∠AFB,
∵AB∥DC,
∴∠ABF=∠BDC,
∴∠AFB=∠BDC,
∴∠AFD=∠EDF,
∵AB=CD=DE,AB∥CD,
∴四边形ABDE是平行四边形,
∴BD∥AE,
∵![]()
∴![]()
∴![]()
∵BD∥AE,
∴![]()
∵∠AFD=∠EDF,
∴∠FAE=∠DEA,
∵∠PAE=∠PEA,
∴∠FAP=∠DEP,
在△APF和△EPD中, 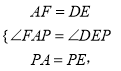
∴△APF≌△EPD,
∴∠AFP=∠DEP,
∵∠AFD=∠EDF,
∴∠PFD=∠PDF,
在Rt△PCD中,PC=PD,
∴![]() ∴
∴![]()
∴![]()
∵![]()
∴![]()
∴∠APF=∠ADB;
(3)由(1)知,△ABP≌△PCE,
∴PC=AB=2,由(1)知,AD+DE=2AB=4,
∴AD=4DE,
∵DB∥PE,
∴△CPE∽△CBD,
∴![]()
∵CB=AD=4DE,CD=AB=2,CE=CDDE=2DE,
∴![]()
∴![]() (由于点E在线段CD上,且CD=2,所以舍去)或
(由于点E在线段CD上,且CD=2,所以舍去)或![]()
即: ![]()
故答案为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
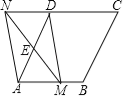
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有营业员16人,销售部为了制定某种商品的月销售定额,统计了这16人某月的销售量如下:
每人销售件数
10
11
12
13
14
15
人数
1
3
4
3
3
2
(1)这16位销售员该月销售量的众数是_____,中位数是_____,平均数是_____.
(2)若要使75%的营业员都能完成任务,应选什么统计量(平均数、中位数和众数)作为月销售件数的定额?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个迷你数独,图中实线划分的区域是一个宫,共有4个宫,每一宫又被虚线分为四个小格.根据图中已经给的提示数字,在其他的空格上填入﹣1、﹣2、﹣3、﹣4的数字.使﹣1、﹣2、﹣3、﹣4每个数字在每一行、每一列和每一宫中都只出现一次.则图中点A的位置所填的数字为( )
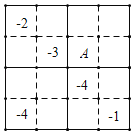
A. ﹣1B. ﹣2C. ﹣3D. ﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的括号内:
﹣2.5,
 ,0,8,﹣2,
,0,8,﹣2,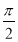 ,﹣1.121121112……
,﹣1.121121112……正数集合:{ };
负数集合:{ };
整数集合:{ };
无理数集合:{ };
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线C1:
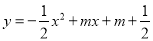
(1) ① 无论m取何值,抛物线经过定点P
② 随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,则点M满足的函数C2的关系式为__________________
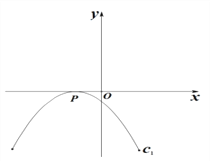
(2) 如图1,抛物线C1与x轴仅有一个公共点,请在图1画出顶点M满足的函数C2的大致图象,平行于y轴的直线l分别交C1、C2于点A、B.若△PAB为等腰直角三角形,判断直线l满足的条件,并说明理由
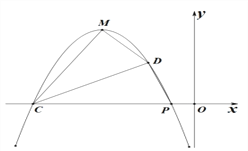
(3) 如图2,二次函数的图象C1的顶点M在第二象限、交x轴于另一点C,抛物线上点M与点P之间一点D的横坐标为-2,连接PD、CD、CM、DM.若S△PCD=S△MCD,求二次函数的解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。
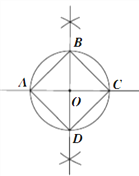
请回答:该尺规作图的依据是____________________________。(写出两条)
相关试题

