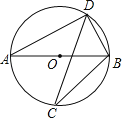
【题目】如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD= ．

参考答案：

【答案】32°

【解析】

试题分析：根据圆周角定理求得∠AOD=2∠ABD=116°（同弧所对的圆周角是所对的圆心角的一半）、∠BOD=2∠BCD（同弧所对的圆周角是所对的圆心角的一半）；根据平角是180°知∠BOD=180°﹣∠AOD，故∠BCD=32°．

解：连接OD．

∵AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°，

∴∠AOD=2∠ABD=116°（同弧所对的圆周角是所对的圆心角的一半）；

又∵∠BOD=180°﹣∠AOD，∠BOD=2∠BCD（同弧所对的圆周角是所对的圆心角的一半）；

∴∠BCD=32°；

另法：∵AB为直径，

∴∠ADB=90°，

∵∠ABD=58°，

∴∠A=90°﹣58°=32°，

∵∠BCD和∠A都是BD所对圆周角，

∴∠BCD=32°．

故答案为：32°．

关闭