【题目】四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BDB.AB∥CD,AC=BD
C.AD∥BC,∠A=∠CD.OA=OC,OB=OD,AB=BC
参考答案:
【答案】A
【解析】
根据正方形的性质以及判定定理对各项进行分析即可.
A. OA=OB=OC=OD,AC⊥BD,能判定;
B. AB∥CD,AC=BD,不能判定;
C. AD∥BC,∠A=∠C,不能判定;
D. OA=OC,OB=OD,AB=BC,不能判定;
故答案为:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是 ( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 三角形两边的垂直平分线的交点到三个顶点距离相等
C. 等腰三角形的两个底角相等
D. 等腰三角形顶角的外角是底角的二倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形两边长是8cm和4cm,那么它的周长是( )
A. 12cm B. 16cm C. 16cm或20cm D. 20cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小华在整理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有同一性质是( )
A.互相平分B.相等
C.互相垂直D.平分一组对角
-
科目: 来源: 题型:
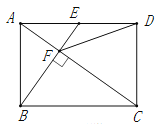
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )

A.CE=
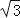 DE B.CE=
DE B.CE= DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
相关试题

