搜索
【题目】小华在整理平行四边形、矩形、菱形、正方形的性质时，发现它们的对角线都具有同一性质是（ ）
A.互相平分B.相等
C.互相垂直D.平分一组对角
参考答案：
【答案】A
【解析】
根据平行四边形、正方形、矩形的性质可知，它们的对角线都具有同一性质是：对角线互相平分．
因为矩形、菱形、正方形都是特殊的平行四边形，而平行四边形的对角线互相平分，所以平行四边形、矩形、菱形、正方形的对角线都具有一个共同的性质，这条性质是对角线互相平分．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知等腰三角形两边长是8cm和4cm，那么它的周长是（ ）
A. 12cm B. 16cm C. 16cm或20cm D. 20cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（ ）
A.OA＝OB＝OC＝OD，AC⊥BDB.AB∥CD，AC＝BD
C.AD∥BC，∠A＝∠CD.OA＝OC，OB＝OD，AB＝BC
-
科目： 来源： 题型：
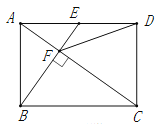
查看答案和解析>>【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝．其中正确的结论有( )
A.4个 B．3个 C．2个 D．1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（ ）
A．CE=
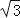DE B．CE=
DE C．CE=3DE D．CE=2DE -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣
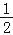，y2）、点C（
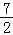，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（ ）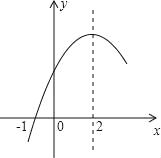
A．2个 B．3个 C．4个 D．5个
相关试题
