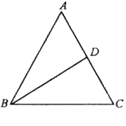
【题目】如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24 cm和30 cm的两部分,求三角形各边的长.
参考答案:
【答案】16,16,22或20,20,14.
【解析】
试题分析:分两种情况讨论:当AB+AD=30,BC+DC=24或AB+AD=24,BC+DC=30,所以根据等腰三角形的两腰相等和中线的性质可求得,三边长为16,16,22或20,20,14.
试题解析:设三角形的腰AB=AC=x
若AB+AD=24cm,
则:x+![]() x=24
x=24
∴x=16
三角形的周长为24+30=54cm
所以三边长分别为16,16,22;
若AB+AD=30cm,
则:x+![]() x=30
x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20,20,14;
因此,三角形的三边长为16,16,22或20,20,14.
-
科目: 来源: 题型:
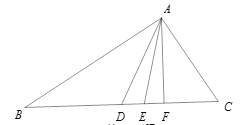
查看答案和解析>>【题目】如图所示,三亚有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站。
(1)当汽车运动到点D时,刚好BD=CD,连接AD,AD这条线段是什么线段?这样的线段在△ABC中有几条?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段?在△ABC中,这样的线段又有几条?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?在△ABC中,这样的线段有几条?
-
科目: 来源: 题型:
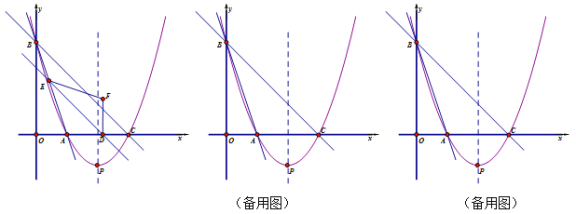
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,对称轴为直线x=2的抛物线经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在直线BC的下方的抛物线上有一动点M,其横坐标为m,△MBC的面积为S,求S关于m的函数关系式,并求S的最大值及此时点M的坐标;
(4)平行于BC的动直线分别交△ABC的边AC、AB与点D、E,将△ADE沿DE翻折,得到△FDE,设DE=x,△FDE与△ABC重叠部分的面积为y,直接写出y与x的函数关系式及自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员各进行10次射击练习,总成绩均为95环,这两名运动员成绩的方差分别是S甲2=0.6,S乙2=0.4,则成绩更稳定的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x2﹣4x﹣5=0;
(2)(x+1)2=2(x+1).
-
科目: 来源: 题型:
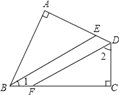
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)∠1+∠2=90°;
(2)BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:

(1)该班共有多少名学生参加这次测验?
(2)求60.5~70.5这一分数段的频数是多少?
(3)若80分以上为优秀,则该班的优秀率是多少?
相关试题

