【题目】如图,∠AOB内有一点P

(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D
(2)写出图中互补的角
(3)写出图中相等的角
(4)试说明图某一对相等.
参考答案:
【答案】(1)见解析;(2)∠O与∠ODP、∠OCP互补;∠CPD与∠ODP、∠OCP互补;∠BDP与∠ODP互补;∠PCA与∠OCP互补;(3)∠O=∠ACP=∠PDB=CPD,∠OCP=∠ODP;(4)∠O=∠ACP,见解析
【解析】
(1)根据平行线的画法作出PC∥OB;根据平行线的画法作出PD∥OA;
(2)根据两直线平行,同旁内角互补;邻补角互补,以及等量代换找出互补的角即可;
(3)根据两直线平行,同位角相等;对顶角相等,以及等量代换找出相等的角即可;
(4)根据平行线的性质即可证明∠O=∠ACP.
(1)如图所示;

(2)∵PC∥OB,
∴∠O与∠OCP互补,∠CPD与∠ODP互补;
∵PD∥OA
∴∠O与∠ODP互补、∠CPD与∠OCP互补;
∵B,D,O在同一直线上,
∴∠BDP与∠ODP互补;
∵A,C,O在同一直线上,
∴∠PCA与∠OCP互补
故图中互补的角有:∠O与∠ODP、∠OCP互补;∠CPD与∠ODP、∠OCP互补;∠BDP与∠ODP互补;∠PCA与∠OCP互补;
(3)∵PC∥OB,
∴∠O=∠ACP,∠CPD=∠PDB,
∵PD∥OA
∴∠O=∠PDB,∠ACP=CPD,
∴∠O=∠CPD,∠OCP=∠ODP,∠ACP=∠PDB,
故图中相等的角有:∠O=∠ACP=∠PDB=CPD,∠OCP=∠ODP;
(4)∵PC∥OB,
∴∠O=∠ACP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
B.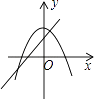
C.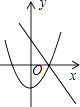
D.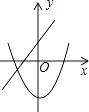
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
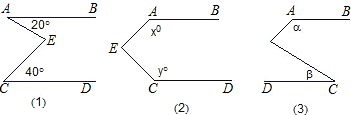
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
-
科目: 来源: 题型:
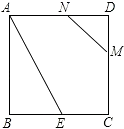
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A.
B.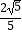
C. 或
或 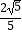
D.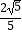 或
或 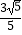
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 .
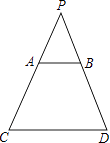
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是 .
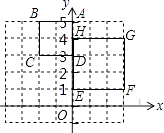
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
相关试题

