【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的中垂线
的中垂线![]() 与
与![]() 的角平分线
的角平分线![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的面积为_______.
的面积为_______.

参考答案:
【答案】![]()
【解析】
过点E作EG⊥AB交AB延长线于G,作EH⊥AC于H,根据角平分线的性质和线段垂直平分线的性质得到EG=EH,EB=EC,然后证明Rt△EGB≌Rt△EHC,Rt△AGE≌Rt△AHE,求出S△EGB=S△EHC,BG=![]() ,得到AG=
,得到AG=![]() ,然后证明四边形AGEH是正方形,根据四边形ABEC的面积等于正方形AGEH的面积计算即可.
,然后证明四边形AGEH是正方形,根据四边形ABEC的面积等于正方形AGEH的面积计算即可.
解:过点E作EG⊥AB交AB延长线于G,作EH⊥AC于H,
∵AE是∠BAC的角平分线,
∴EG=EH,
∵DE是线段BC的垂直平分线,
∴EB=EC,
在Rt△EGB和Rt△EHC中,![]() ,
,
∴Rt△EGB≌Rt△EHC(HL),
∴BG=CH,S△EGB=S△EHC,
在Rt△AGE和Rt△AHE中,![]() ,
,
∴Rt△AGE≌Rt△AHE(HL),
∴AG=AH,
∴AB+BG=AC-CH,
∴3+BG=4-BG,
∴BG=![]() ,
,
∴AG=AB+BG=![]() ,
,
∵∠GAC=∠AGE=∠AHE=90°,
∴四边形AGEH是矩形,
∵AG=AH,
∴矩形AGEH是正方形,
∴S四边形ABEC=S四边形ABEH+S△EHC=S四边形ABEH+S△EGB=S正方形AGEH=AG2=![]() ,
,
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形
(1)如图1,在半对角四边形ABCD中,∠B=
 ∠D,∠C=
∠D,∠C= ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,当DH=BG=2时,求⊙O的直径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2-
 x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0)
x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0)(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,记点M到线段BC的距离为d,当d取最大值时,求出此时M点的坐标;
(4)若点P是抛物线上一点,点E是直线y=-x+1上的动点,是否存在点P、E,使以点A,点B,点P,点E为顶点的四边形是平行四边形?若存在,请直接写出点E坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小王和小李都想去体育馆,观看在我县举行的“市长杯”青少年校园 足球联赛,但两人只有一张门票,两人想通过摸球的方式来决定谁去观看,规则如下: 在两个盒子内分别装入标有数字 1,2,3,4 的四个和标有数字 1,2,3 的三个完全相 同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于 6,那 么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平.”你认同他的说法吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数是白球个数的2倍少5个,已知从袋中摸出一个球是红球的概率是
 .
.(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是_________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中小正方形的边长为1,
 (0,4).
(0,4).
(1) 在图中标出点
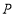 ,使点
,使点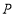 到点
到点 ,
, ,
, ,
, 的距离都相等;
的距离都相等;(2) 连接
 ,
, ,
, ,此时
,此时 是___________三角形;
是___________三角形;(3) 四边形
 的面积是___________.
的面积是___________.
相关试题

